
Wenn es ums Quantencomputing geht, gehören bereits die trivialsten Fragen à la „Worum geht es?“ oder „Für was soll es denn gut sein?“ zu denjenigen Fragen, die auch einen Experten auf diesem Gebiet ganz schön auf dem falschen Fuß erwischen können… Wird dann noch nachgefragt, was denn eigentlich die Grundidee des Quantencomputers sei, so gerät der Gefragte erst mal in eine nachdenkliche Pose 😳, auf die eine mehr oder weniger strukturierte Antwort folgt. So heißt es beispielsweise, Quantencomputer würde gleichzeitig mit 0 und 1 von einem Bit rechnen, könne, gefragt nach einer Seite einer Münze, deren beide Seiten parallel anschauen etc. – alles Antworten, die dem Zuhörer bzw. Leser womöglich nicht unbekannt sind. Eine Frage drängt sich hierbei allerdings sofort auf, nämlich, wie soll ich denn mit etwas rechnen, von dem ich nicht einmal weiß, ob es 0 oder 1 ist? Welchen Informationsgehalt sollte solch ein „Qubit“ haben, wenn es mir nicht einmal die einfachste Frage beantworten und somit die Information liefern kann, ob es denn 0 oder 1, schwarz oder weiß etc. ist ??
.

Natürlich ist man angesichts solcher Fragestellungen geneigt, den legendären Richard Feynman zu zitieren, der in einer unnachahmlichen Manier das QC mit Welleneffekten erklärte, die er in seinen berühmten Vorlesungen förmlich zelebrierte. Aber so sehr ich Richard Feynman verehre, will ich die grundlegend andere Interpretation, nämlich die von David Deutsch, als Grundlage für dieses Tutorial hernehmen. Die Deutsch’sche Erklärung des QC zielt auf Parallelwelten ab, was mir persönlich unnötig abstrakt ist. Aber sie liefert eine Möglichkeit, anhand des sog. Deutsch-Problems den Gedankengang seines geistigen Vaters und eines weiteren QC-Ideengebers nachvollziehen zu können. Hinterher kann der Leser selbst entscheiden, ob die physikalische Erklärung für das hier diskutierte Phänomen mehr bei den Welleneffekten oder eher in den Parallelwelten zu suchen ist.
Um diesem Tutorial folgen zu können sind wenigstens rudimentäre Kenntnisse in Sachen Quanten-Bit und -Register, Tensorenalgebra mit Ket-Schreibweise ![]() etc. von Vorteil. Im Zweifelsfall möge sich der Leser aus dem reichlich vorhandenen Online-Angebot bedienen; ein Blick ins Whitepaper „Sicherheit von transObjects® und loggPRO®.net gegenüber Quantencomputing“ mit den dortigen FAQ’s mag da ebenfalls hilfreich sein.
etc. von Vorteil. Im Zweifelsfall möge sich der Leser aus dem reichlich vorhandenen Online-Angebot bedienen; ein Blick ins Whitepaper „Sicherheit von transObjects® und loggPRO®.net gegenüber Quantencomputing“ mit den dortigen FAQ’s mag da ebenfalls hilfreich sein.
Das (klassische) Deutsch-Problem
.
Gegeben sei eine deterministische Funktion ![]() in Form einer Bit-zu-Bit Abbildung:
in Form einer Bit-zu-Bit Abbildung:
![]()
➡ die Basis 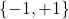 anstatt der üblichen
anstatt der üblichen 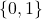 sollte dem Leser den Abgleich mit dem Youtube-Video von David Deutsch erleichtern.
sollte dem Leser den Abgleich mit dem Youtube-Video von David Deutsch erleichtern.
.
Physikalisch gesehen liegt ![]() in Form einer Blackbox, also eines „Orakels“, vor. Die Aufgabe lautet nun, algorithmisch herauszufinden, wie unser Orakel „tickt“, d.h. welche „Antworten“ es auf die beiden möglichen „Fragen“ -1? und +1? liefert:
in Form einer Blackbox, also eines „Orakels“, vor. Die Aufgabe lautet nun, algorithmisch herauszufinden, wie unser Orakel „tickt“, d.h. welche „Antworten“ es auf die beiden möglichen „Fragen“ -1? und +1? liefert:
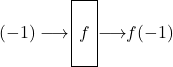 sowie
sowie 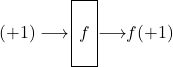
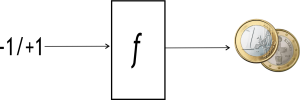
Wir dürfen nicht in das Orakel hineinschauen – ganz davon abgesehen, dass es u.U. ein aussichtsloses Unterfangen sein könnte, das Innere unseres Orakels im Hinblick auf die zu lösende Aufgabe zu analysieren. Was wir aber einwandfrei tun dürfen, ist Inputs gegen das Orakel zu „fahren“ und so die Outputs zu erfragen. Nach zweifachem Bemühen des Orakels mit -1 und +1 hat dieses offensichtlich keine Geheimnisse mehr vor uns: Wir kennen dann die beiden Antworten ![]() bzw.
bzw. ![]() und können somit die vollständige Funktionstabelle für
und können somit die vollständige Funktionstabelle für ![]() angeben.
angeben.
Soweit so gut. Wir können also das Orakel „entziffern“, indem wir ihm zwei der möglichen zwei Fragen stellen (bzw. wir können alle Informationen über die darin schlummernde Münze gewinnen, indem wir deren beide Seiten anschauen lassen). Indes erscheint die Frage, ob es nicht mit einem nur einmaligen Bemühen des Orakels (bzw. mit dem Anschauen nur einer Seite der Münze) getan sein könnte, erstens absurd und zweitens unter allen Umständen zu verneinend ➡. Denn, was die Sinnhaftigkeit einer solchen Fragestellung anbelangt, so können wir doch zu deren Rechtfertigung z.B. annehmen, dass das Orakel sehr langsam ist und/oder sehr teuer, so dass es sich durchaus lohnt über so etwas nachzudenken (Psychologen nennen so etwas, glaube ich, „Rechtfertigungszufriedenheit“ 😳).
➡ An dieser Stelle sei vorweggenommen, dass auch ein Quantencomputer vollkommen machtlos ist gegenüber einer solchen Vorgabe: auch der muss nämlich das Orakel zweimal bemühen. Das, was als „Deutsch-Problem“ bezeichnet wird und wovon der Leser möglicherweise als „in nur einem Schritt“ lösbar gehört hat, ist eine modifizierte Abfrage des Orakels und zwar unter dem Blickwinkel der wellentechnischen Überlagerung (Interferenz) 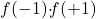 – s. ff.
– s. ff.
.
Diese Erkenntnis zeigt zunächst mal, dass QC nicht alle Rechenoperationen beschleunigen kann – nur einige davon, was wir im Folgenden noch sehen werden. Das macht die Frage nach dem Wesen der quantentheoretischen Berechenbarkeit entsprechend schwierig. Insbesondere lässt sich kein fester Beschleunigungsfaktor fürs QC gegenüber dem klassischen Computing angeben und auch Fragen der Berechenbarkeit sind prinzipiell nicht eindeutig zu beantworten. Der grundsätzlich probabilistische Charakter der QC macht diese Fragen alles andere als einfach.
.
Eine geeignete Gatterschaltung für unser Orakel erscheint zwar auf den ersten Blick trivial:
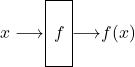
…hat aber einen ganz entscheidenden Konstruktionsfehler, nämlich die Nicht-Reversibilität. Diese „Undo“-Funktionalität wird aber gerade in der Quanteninformatik aus einer Reihe von Gründen gefordert. Wir brauchen also eine Gatterschaltung, die den Input „konserviert“:
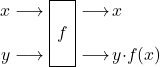 was bei fester Setzung
was bei fester Setzung ![]() das Resultat auf dem 2. Bit liefert:
das Resultat auf dem 2. Bit liefert: 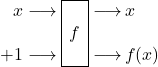
➡ An dieser Stelle kam ein entschiedenes „Moment mal“ von einem sehr versierten Zuhörer: „Ist es nicht eine unzulässige Modifikation des Orakels, so dass insbesondere ein QC bessere Chancen hat?“ „Warum?“ „Nun, immerhin können wir jetzt beide Inputs „gegen die Kiste“ fahren und ein QC soll ja mit beiden Bits irgendwie rechnen können?“
.
In der Tat wäre ein QC bei einer nicht-reversiblen Variante des Schaltkreises völlig machtlos gegenüber jedweder Variante des Deutsch-Problems. Auf der andere Seite ist ganz einfach zu zeigen, dass ein so modifizierter Schaltkreis dem klassischen Computer überhaupt nicht behilflich sein kann. Die Ursache hierfür liegt darin, dass – im Gegensatz zum QC – die klassischen Bits per se nicht miteinander verschaltet sind. Somit nutzt das 2-Bit-Register nichts, da das erste Bit das ohnehin schon bekannte Bit ist, also müssen wir so oder so unser Orakel zweimal bemühen.
.
Nun wird sich insbesondere David Deutsch früher mal gefragt haben, ob denn nicht eine Möglichkeit besteht -1 und + 1 irgendwie in Parallelwelten gegen das Orakel fahren zu können, wobei auch er an die wellentechnische Überlagerung gedacht haben dürfte. Dabei war die Grundidee diejenige, nicht nur die Inputs miteinander zu überlagern sondern auch und insbesondere die Outputs. Wellentechnische Überlagerung bedeutet aber mathematisch gesehen stets eine algebraische Verknüpfung der beiden Funktionswerte:
![]()
wobei diese Verknüpfung entweder additiv oder multiplikativ sein kann. Das wir aber zufälligerweise die Basis so gewählt haben, wie wir sie gewählt haben, können wir uns mit Fug und Recht auf die multiplikative Variante zurückziehen:
![]()
Die Aufgabe, die wir uns nun stellen, kann wie folgt modifiziert und vereinfacht werden: Ich muss nicht wissen, wie die Funktionstabelle im Einzelnen aussieht – es reicht mir zu wissen, ob die Funktion konstant ist oder nicht. Auf die Münze übertragen heißt es, ich muss nicht wissen, wie herum die Münze liegt – es reicht zu wissen, ob sie fair ist oder nicht.
Wie bereits im letzten Einschub angedeutet, ist das Deutsch-Problem, also die Berechnung von ![]() , in keinem Schaltkreis durch einen klassischen Computer in nur einem Schritt lösbar. Im nächsten Kapitel konstruieren wir einen QC-Schaltkreis, mit dem Ziel, diese Aufgabe in nur einem Schritt zu lösen.
, in keinem Schaltkreis durch einen klassischen Computer in nur einem Schritt lösbar. Im nächsten Kapitel konstruieren wir einen QC-Schaltkreis, mit dem Ziel, diese Aufgabe in nur einem Schritt zu lösen.
Das quantentheoretische Deutsch-Problem
.
Im vorherigen Kapitel haben wird das Deutsch-Problem ausführlich vorgestellt und eine reversible, klassische Gatterschaltung, die dieses Problem auf algorithmischem Wege löst, konstruiert:
.

.
Ebenso haben wir festgestellt, dass die Lösung des eigentlichen Deutsch-Problems, also die Ermittlung von ![]() , stets ein zweifaches Bemühen des Orakels erfordert und zwar für die beiden Inputwerte
, stets ein zweifaches Bemühen des Orakels erfordert und zwar für die beiden Inputwerte ![]() sowie
sowie ![]() :
:
.
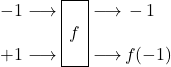 sowie
sowie 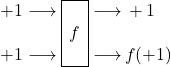
.
Doch mit diesem Umstand mochte sich seinerzeit David Deutsch nicht so recht anfreunden. Vielmehr hatte er vehement vermutet, dass es gerade in der Quantenwelt doch noch möglich sein müsste, beide Inputwerte gleichzeitig – wenn auch irgendwie in „Paralleluniversen“ – gegen das Orakel zu fahren und die so errechneten Resultate in der „unsrigen“ Welt in einer quantenmechanischen Superposition zusammen zu tragen. Die anschließende Bellsche Messung sollte dann das gesuchte Produkt ![]() liefern.
liefern.
Der korrespondierende Schaltkreis müsste dann in etwa folgendermaßen aussehen:
.

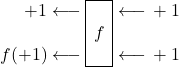
.
Hier kommen beide Resultate wunderschön, ja förmlich bildhaft zusammen. Die Sache hat allerdings einen Haken und zwar, wir nutzen eine identische Kopie unseres Orakels, was nichts anderes ist, als dessen zweifaches Bemühen, wenn auch gewissermaßen „parallel“. Aber vielleicht lässt sich dieser Schritt gerade in der Quantenwelt irgendwie überschlagen? Mal sehen. Die Grundidee scheint erst mal durchaus erfolgversprechend.
Allerdings, wenn wir einen QC-Schaltkreis hierfür konstruieren wollen, müssen wir erst einmal eine gewaltige Konzession zugunsten von QC machen, nämlich unser Orakel muss ein Quantenorakel werden und darf die Qubits, die wir nun anstatt der klassischen Bits gegen das Orakel fahren wollen, nicht dekohärieren, also deren quantenmechanische Überlagerung zugunsten eines Basiszustandes zerstören.
Zunächst liegt es nahe, die korrespondierende unitäre Matrix dem klassischen Orakel von vorher nachzubilden:
.
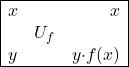
.
Versuchen wir jetzt die korrespondierenden Qubits gegen ein solches Orakel zu fahren, so stellen wir rasch fest, dass auch damit nicht wirklich etwas gewonnen ist. Selbst David Deutsch und auch andere Forscher machten zunächst diese frustrierende Erfahrung… 🙄 Egal was Sie versucht hatten, benötigte deren Algorithmus ebenfalls zwei Funktionsaufrufe oder aber lieferte das Resultat nur mit einer gewissen Wahrscheinlichkeit; bei 50% natürlich völlig nutzlos…
Erst 1998 gelang R. Cleve, A. Ekert, C. Macchiavello und M. Mosca mit Hilfe der nachfolgenden Gatterschaltung die deterministische (!) Lösung des Deutsch-Problems bei einem nur einmaligen Bemühen des Orakels:
.

.
Die Grundidee dabei ist gleichermaßen genial wie verrückt. Zunächst wird hier das erste Qubit (das im Falle der klassischen Gatterschaltung lediglich den Input „konservierte“), dazu benutzt, den zweiten Inputwert in das System mit hineinzubringen um ihn mit dem ersten in Superposition zu bringen. Das Widersinnige dabei: dieses Qubit, das zwei Hadamard Gatter ➡ durchläuft (die sich ja definitorisch aufheben!) und scheinbar keine Veränderung im ![]() erfährt, hält am Ende das deterministische Resultat von
erfährt, hält am Ende das deterministische Resultat von ![]() … 💡
… 💡
➡ Hadamard-Gatter haben folgende Wirkung auf unsere Qubits:
.
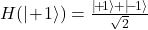
.
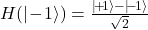
.
Kann es stimmen? Nun, es bleibt nicht anderes übrig als es nachzurechnen. Zunächst ist anzumerken, dass das 2-Qubit-Register sich von Anfang in einer Superposition befindet, so dass beide Qubits einander „spüren“. Algebraisch gesehen wird dieser Tatsache durch das Tensorprodukt Rechnung getragen:
![]()
Danach durchlaufen beide Qubits die Hadamard-Transformation mit folgendem Resultat:
![]()
Nach tensoralgebraischem Ausmultiplizieren erhalten wir – nicht wirklich überraschend – eine Superposition aller 4 Basiszustände unseres Q-Registers:
![]()
Danach fahren wir damit gegen unsere „Kiste“: erstes Qubit bleibt unverändert ![]() , zweites wird zu
, zweites wird zu ![]() :
:
![]()
Bei näherem Hinsehen zeigt sich, dass unser Orakel bereits nach diesem einmaligen Aufruf alles hergegeben hat, was wir von ihm wissen wollten. Wie das? Nun, betrachten wir die zwei möglichen Resultate von ![]() , nämlich
, nämlich
(1) ![]()
sowie
(2) ![]() .
.
Im ersteren Falle befindet sich unser Q-Register im Zustand:
(1) 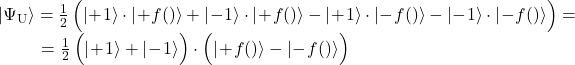
andernfalls im Zustand:
(2) 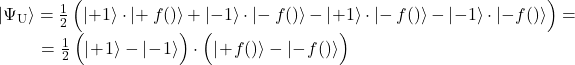
Wie durch eine Zauberei ist das 2. Qubit relativ uninteressant geworden, während das erste haargenau die Hadamard-Transformation von den beiden Input-Werten enthält: Im Falle (1) ist es ![]() und im Falle (2)
und im Falle (2) ![]() 💡. Eine erneute Anwendung der Hadamard-Transformation flippt das erste Qubit in den Zustand
💡. Eine erneute Anwendung der Hadamard-Transformation flippt das erste Qubit in den Zustand ![]() bzw.
bzw. ![]() und die anschließende Messung liefert dann das gesuchte
und die anschließende Messung liefert dann das gesuchte ![]() . Sensationell 😯 !!!
. Sensationell 😯 !!!
Diskussion
http://qudev.phys.ethz.ch/content/courses/QSIT06/presentations/Deutsch-Josza.pdf
