Hawking-Strahlung

Rainer A. StawarzAG Energetik, Allgemein

Ich werde häufig gefragt, was denn dieses etwas kryptisch anmutende Logo links oben zu bedeuten habe. Da wäre eine Art Kompass, dessen „Meridian“ eine Gleichung ausgerechnet an deren Gleichheitszeichen durchkreuzt… schon irgendwie seltsam 😉

Nun, meine Antwort, die ich normalerweise hierauf gebe – nämlich dies sei die Hawking-Strahlung – ist nicht ganz exakt. Denn in Wahrheit handelt es sich um die sog. Bekenstein-Hawking-Gleichung, die die Entropie S, eines schwarzen Lochs in Abhängigkeit von der Fläche A seines Ereignishorizonts beschreibt:

S=\frac{c^3A}{4{\hbar}G}  bzw. S=\frac{A}{4l_\text{P}^2} ➡ wenn wir die Planck-Länge  l_\text{P}=\sqrt{G\hbar/c^3} bemühen.

➡ Insbesondere anhand der zweiten Gleichung ist unschwer zu erkennen, dass es sich hierbei um eine dimensionslose Zahl handelt. In der Tat liefert erst die Multiplikation mit der Boltzmann-Konstanten die gewohnte Entropie in der Dimension [J/K].
.

Da die übrigen Größen in der Bekenstein-Hawking-Gleichung allesamt Naturkonstanten ➡ sind, entspricht die Linearität S~A Bekensteins (Gedanken-) Beobachtung vom Eintritt eines Objekts ins schwarze Loch: Die Entropie außerhalb des schwarzen Loches nimmt um die des eintretenden Objektes ab, während das schwarze Loch entsprechend „größer“ wird. Somit hängt dessen Entropie einzig und alleine von der Fläche seines Ereignishorizonts ab.

➡ Lichtgeschwindigkeit 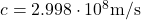c=2.998\cdot10^{8}\text{m/s}
➡ Plancksches Wirkungsquantum: 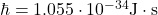\hbar=1.055\cdot10^{-34}\text{J}\cdot\text{s}
➡ Gravitationskonstante: 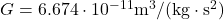G=6.674\cdot10^{-11}\text{m}^3\text{/(kg}\cdot\text{s}^2)
➡ Boltzmann-Konstante: 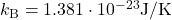k_\text{B}=1.381\cdot10^{-23}\text{J/K}
➡ Planck-Länge: 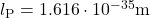l_\text{P}=1.616\cdot10^{-35}\text{m}
.

Die so postulierte Entropie verlieh schwarzen Löchern zunächst quasi „gewöhnliche“ thermodynamische Eigenschaften, so dass wir uns im Rahmen unserer „AG Energetik“ auch mit solch bizarren Objekten gerne beschäftigen mögen…:mrgreen: Denn bei der Verschmelzung zweier schwarzer Löcher beispielsweise ist die resultierende Entropie stets höher als die Summe beider Einzelentropien, was konform mit dem 2. Gesetz der Thermodynamik geht (allerdings verhindert es wiederum die Aufspaltung des schwarzen Lochs ohne entsprechende „Zufuhr“ an Entropie). Doch die wohl wichtigste Eigenschaft, die dadurch schwarzen Löchern verliehen wurde, war die „normale“, insbesondere endliche Temperatur ➡ sowie die wegen thermodynamischem Gleichgewicht mit der unmittelbaren Umgebung implizierte Strahlung – die Hawking-Strahlung eben.

➡ Diese beträgt im Falle von supermassiven schwarzen Löchern, gem. Auflösung der Gleichung nach Temperatur mit Hilfe der Schwarzschild-Metrik, nur Bruchteile eines Kelvins. Lediglich kurz vor deren „Ableben“ (dem vollständigen „Ausstrahlen“) sind schwarze Löcher etwas wärmer:
.
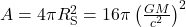A=4\pi{R_\text{S}^2}=16\pi\left(\frac{GM}{c^2}\right)^2  (für stationäre und kugelförmige schwarze Löcher), folglich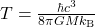  T=\frac{\hbar{c^3}}{8{\pi}GMk_\text{B}}
.

In der Tat war es Stephen Hawking, der das Paradoxon der Abgabe von Materie durch ein definitorisch nur absorbierendes Objekt („schwarzes“ Loch eben) mittels der nach ihm benannter Strahlung auflöste. Indes hat er es wohl seinem waghalsigen quanten- wie relativitätstheoretischen Ansatz zu verdanken, dass die Bekenstein-Hawking-Entropie als eine Erfindung von Bekenstein und Hawking gilt und die Bekenstein-Hawking-Gleichung eher Hawking als Bekenstein zugeschrieben wird (s. etwa BBC-Reportage „Hawkings-Dilemma„).

In Wahrheit hatte Hawking mit dem Übergang der Entropie (und erst recht der Information!) in den Ereignishorizont stets so seine Probleme und das trotz der so grandiosen Bestätigung von Bekensteins Vermutung. Sein Problem damit kulminierte seinerzeit in dem Postulat des Informationsverlustes beim Eintritt ins schwarze Loch, was eine über 30 Jahre andauernde Kontroverse rund um das sog. Informationsparadoxon hervorgerufen hatte.

Soweit so gut – schwarze Löcher sind also gar nicht so schwarz. Heißt es aber, dass sich jedes schwarze Loch früher oder später ausstrahlt, sofern es nicht zwischendurch wieder „Nahrung“ bekommt? Nun, die Antwort ist zunächst, dass schwarze Löcher selbst im intergalaktischen Raum sehr wohl „Nahrung“ bekommen und zwar wenn nicht von anderen Himmelskörpern, so doch spätestens von der Hintergrundstrahlung (auch „Reliktstrahlung“). Die Frage, die wir uns in einer der anspruchsvolleren Aufgaben unserer „AG Energetik“ nun stellen, ist, ab welcher Masse übersteigt die innergalaktische Hintergrundstrahlung (2.8 Kelvin) die Hawking-Strahlung eines nicht-rotierenden schwarzen Loches?

Zunächst lösen wir die Bekenstein-Hawking-Gleichung nach Masse auf:

M=\frac{\hbar{c^3}}{8{\pi}GTk_\text{B}}

Zwischendurch überprüfen wir mal die Dimension, um ganz sicher zu gehen, dass wir da auf dem richtigen Track sind:

\left[ M \right]=\frac{\text{J}\cdot\text{s}\cdot\text{m}^3\cdot\ctext{s}^{-3}}{\text{m}^3\text{/(kg}\cdot\text{s}^2)\cdot\text{K}\cdot\text{J/K}}=\text{kg}

Also passt alles – wir erhalten unser Resultat korrekterweise in Kilogramm. Jetzt müssen wir nur noch die Werte in die Gleichung einsetzen und dürfen dann auf das Resultat gespannt sein:

M=\frac{1.055\cdot10^{-34}\cdot(2.988)^3\cdot10^{24}}{8\cdot3.14\cdot6.674\cdot10^{-11}\cdot2.8\cdot1.381\cdot10^{-23}}=\frac{28.479}{648.272}\cdot10^{24}=4.393\cdot10^{22}\,\text{kg}

Demnach ist es die Größenordnung des Erdmondes. Ist also die Masse des schwarzen Loches geringer als der von uns errechnete Wert, geht es mit ihm „bergab“ bis es irgendwann einmal tatsächlich verschwindet, sich also restlos „ausstrahlt“. Ist hingegen die Masse höher, dann reicht alleine die Hintergrundstrahlung dafür aus, um ein beständiges Wachstum aufrecht zu erhalten.