Ein Freund von mir hatte sich neulich einen Traum erfüllt, indem er für sich und seine frisch gebackene Familie ein Eigenheim gebaut hatte. Voller Erwartungsfreude widmete er sich nächtelang einer detaillierten Planung, damit sich ja nicht irgendwelche „grundlegenden“ Fehler in die so einmalig anspruchsvolle Konstruktion 😉 hineinschleichen. Folgerichtig kannte seine Freude kaum noch Grenzen, als er auf eine neue geniale Erfindung gestoßen war, nämlich „Luftwärmepumpen“. Diese Dinge würden mit einem Wirkungsgrad von bis zu 400% arbeiten und somit seien die ohnehin überschaubaren Anschaffungskosten einer solchen Pumpe durch die Einspareffekte bei der Heizung schnell wieder „drin“.

Die erste Rechenaufgabe der vorliegenden AG-Energetik besteht also darin, die Frage zu beantworten, ob mein Freund zurecht solch gewaltige Einsparpotentiale gegenüber der konventionellen Erdgasheizung erwartet. Mit anderen Worten, „rechnet“ sich eine solche Luftwärmepumpen denn überhaupt?

Eigentlich könnten wir es uns ganz einfach machen. Denn wenn der Wirkungsgrad (also das Verhältnis der investierten elektrischen Energie zu der gepumpten Wärme) „bis zu“ 400% beträgt, dann muss man schon einen sehr günstigen Stromtarif haben, um wenigstens ein Nullsummenspiel daraus zu machen: eine kWh Gas kostet unter 0.07€ während der Strom irgendwo bei 0.28€ herumpendelt (Stand 2015). Also alleine von dem her rechnet sich eine solche Luftwärmepumpe nicht. Wir wollen es aber genauer wissen, denn schließlich kann es auch andere Gründe geben, die für eine solche Vorrichtung sprechen – z.B. Umweltbelange oder auch die Bestrebung, überhaupt kein Gas oder Heizöl verwenden zu wollen.

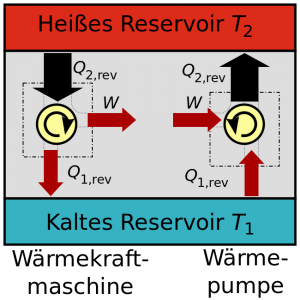
Doch anstatt es direkt zu rechnen, versuchen wir uns dieser Problematik von einer ganz anderen Seite her zu nähern, nämlich über den „komplementären“ Prozess, den sog. Carnot-Prozess. Der Name geht auf den französischen Ingenieur Nicolas Léonard Sadi Carnot zurück, der im 19. Jahrhundert eine unerbittliche und bis heute wenig verinnerlichte Gesetzmäßigkeit⇓ feststellte, nämlich, dass bei jeder Umwandlung von thermischer Energie in eine höherwertige Energieform (z.B. mechanische oder elektrische Energie) der Wirkungsgrad durch die Temperaturdifferenz zwischen der Wärmequelle (z.B. Wasserdampf) und der Senke (z.B. Kühlung oder schlicht Umgebung) begrenzt ist. Im Idealfall, d.h. ohne Prozessverluste, bei Einsatz von Idealgasen etc. beträgt dieser sog. Carnot-Wirkungsgrad:

 ; gemeint sind stets absolute Temperaturen, also die Kelvin-Werte. Der Pfeil nach rechts symbolisiert den rechtslaufenden Prozess – s. ff.

ist demnach umso höher, je mehr wir „anheizen“, jedoch niemals 100%. Dies hat – um das hier zum weiß ich nicht wievielten Male zu betonen – nichts mit technischen Unzulänglichkeiten unserer Motoren zu tun sondern ist von grundlegender Natur; genauer gesagt ist es eine Folge aus den Gesetzen der Thermodynamik.

Was hat das alles mit der Luftwärmepumpe von meinem Freund zu tun, wird sich vielleicht der Leser fragen? Nun, drehen wir den Carnot-Prozess einfach mal um, so stellen wir fest, dass dabei genau das Gegenteil zum ursprünglichen Prozess passieren sollte, nämlich eine Umwandlung von mechanischer Energie in Wärme. Wenn dem aber so ist, wäre das exakt unsere Luftwärmepumpe! Mehr noch, der umgekehrte Carnot-Prozess (andere Bezeichnungen für „umgekehrt“ lauten „komplementär“ oder „linkslaufend“, manchmal auch „Joule-Thomson-Prozess“) kann in der Tat Wirkungsgrade von über 100% erreichen!

Also doch gute Nachrichten für meinen Freund? Mitnichten! Denn erstens wird an dieser Stelle gefliessentlich übersehen, dass in dem linkslaufenden Prozess zunächst die höherwertige Energie (Strom!) benötigt wird, die wiederum stets teurer eingekauft werden muss (wie oben bereits gesehen). Zweitens, was noch gravierender ist: würden wir beide Prozesse aneinander reihen, so wäre der Wirkungsgrad durch den Kehrwert des Carnot-Wirkungsgrades begrenzt:

Mit anderen Worten, die sagenumwobenen Wirkungsgrade von über 100% gibt es zwar, aber nur dann, wenn die Temperaturdifferenz begrenzt bleibt. Das kann wiederum Außentemperaturen bedeuten, bei denen man gar keine Heizung mehr braucht! Und wenn es da draußen richtig kalt ist, arbeitet eine Luftwärmepumpe extrem unwirtschaftlich 😳 – übrigens ein Effekt, dem die Erdwärmepumpen-Hersteller zu entgehen versuchen, indem sie die Tanks in der Erde verbuddeln, wo auch bei klirrender Kälte +4°C herrschen. Und setzt man dann noch großflächige Heizung ein (Fußbodenheizung beispielsweise), so kann man den Temperaturbereich in der Tat ein wenig im Zaum halten; der Aufwand von so etwas ist freilich enorm.

Für meinen Freund heißt es demnach schlicht und ergreifend, er zahlt gegenüber einer konventionellen Heizung richtig drauf, weil eine Luftwärmepumpe (wie jede Wärmepumpe übrigens auch) teure Input-Energie benötigt und darüber hinaus starken Temperaturschwankungen der Außenluft unterliegt.

Und die Umwelt? Die hat leider auch nichts davon, solange der Strom sowie die allermeiste Primärenergie überwiegend aus fossiler Verbrennung stammen.