»

Quelle © dpa
Stellen wir uns vor, keine geringere als die „Sovereign Maersk“ ➡ wird demnächst in einen Containerhafen reinlaufen, wo ihre 7.500 Container gelöscht werden sollten. Die Aufgabe für das hafenweite Dispositionssystem besteht nun darin, für all die Container mitsamt den unterschiedlichen Inhalten geeignete Stellplätze zu finden und diese zu reservieren. Dabei handelt es sich selbstverständlich um rein elektronische Vorgänge, die mit der heutigen IT auch machbar erscheinen – entsprechende Datenbanken mit allumfassenden Informationen über die gegenwärtige Belegung des Containerhafens stets vorausgesetzt. Dass aber eine solche Aufgabe trotz modernster IT alles andere als trivial ist und mit noch so schnellen Prozessoren immer noch laufzeitkritisch werden kann, sei an dieser Stelle schon mal vorweggenommen: Das vorliegende Tutorial wird zeigen, dass das Durchstöbern eines Containerhafens nach geeigneten Lagerplätzen für ein paar Tausend Container naturgemäß laufzeitkritisch ist!
➡ Die Sovereign Maersk – Schiffe zählen zu den Post-Panamax-Containerschiffen und verfügen über eine Kapazität von 6600 TEU (beladene Container mit je 14 Tonnen Gewicht), beziehungsweise 8160 TEU an echten Stellplätzen.
.

Quelle © N. Trentmann @welt.de
Eine einfache Überlegung, die an dieser Stelle nicht näher vorgestellt werden sollte, die aber durch Beobachtungen im Alltag durchaus gestützt wird, zeigt, dass ein Containerhafen im Schnitt in etwa so viele disponible Containerplätze haben sollte, wie der (Container-) Jahresumsatz ist. Im Falle von Shanghai wären es 40.000 Stellplätze durchschnittlich. Unsere Aufgabe anhand des Beispiels von Shanghai besteht demzufolge darin, eine Datenbank mit 40.000 Einträgen zu durchlaufen (zu „iterieren“) und die Eignung des jeweiligen Stellplatzes für den einzulagernden Container zu prüfen. Zu der äußerst diffizilen „Eignungsprüfung“ ![]() ➡ als Funktion von einer Reihe von Stellplatz- und Container-Parametern später mehr.
➡ als Funktion von einer Reihe von Stellplatz- und Container-Parametern später mehr.
Für jeden Kenner der Algorithmentheorie ist dieser Fall klar: die Laufzeit einer solchen Datenbank-Iteration geht linear mit dem Umfang derselben, was mit dem Operator ![]() markiert wird (das „
markiert wird (das „![]() “ steht hier für unsere 40.000 Container-Stellplätze). Demzufolge ist die Laufzeit einer vollen Datenbank-Iteration über 40.000 virtuelle „Stellplätze“ offensichtlich
“ steht hier für unsere 40.000 Container-Stellplätze). Demzufolge ist die Laufzeit einer vollen Datenbank-Iteration über 40.000 virtuelle „Stellplätze“ offensichtlich ![]() – stets vorausgesetzt, dass das
– stets vorausgesetzt, dass das ![]() (also die Latenzzeit einer Eignungsprüfung
(also die Latenzzeit einer Eignungsprüfung ![]() ) für alle Stellplätze
) für alle Stellplätze ![]() gleich ist, was in der Praxis weitgehend der Fall ist.
gleich ist, was in der Praxis weitgehend der Fall ist.
➡ Die Einzeleignungsprüfung 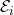 ist das entscheidende Momentum für den vorliegenden Algorithmus. Formell handelt es sich um eine Funktion, die eine Reihe von Stellplatz-Paramatern auf „0“ („nicht geeignet“) oder „1“ („geeignet“) abbildet:
ist das entscheidende Momentum für den vorliegenden Algorithmus. Formell handelt es sich um eine Funktion, die eine Reihe von Stellplatz-Paramatern auf „0“ („nicht geeignet“) oder „1“ („geeignet“) abbildet:  . Natürlich kann man die Funktion erweitern, indem man eine Art Punktesystem macht und damit eine differenzierende Antwort heraus bekommt.
. Natürlich kann man die Funktion erweitern, indem man eine Art Punktesystem macht und damit eine differenzierende Antwort heraus bekommt.
.

Im Folgenden setzen wir für ![]() 0.1ms=100μs (Mikrosekunden) an und nehmen somit den künftigen technischen Fortschritt vorweg. Denn alleine die I/O-Operationen auf den modernsten Datenträgern dauern derzeit (Stand Anfang 2019) ungefähr so lang. Unter dieser Annahme dauert eine Datenbank-Iteration 4 Sekunden lang und das hört sich erst mal nicht dramatisch an. Allerdings dürfen wir die übrigen 7499 Container 😀 nicht vergessen, die ebenfalls auf ihre Iterationen warten. Claro, nicht jeder Container wird es brauchen. Denn wenn ich mehrere nahezu identisch beladene rechne, weiß ich aus der ersten Iteration (durch das Punktesystem), was die geeigneten Stellplätze für die anderen sind. Dennoch müssen wir von dem berühmten worst case ausgehen, denn nur dieser beschreibt die immanente Komplexität eines Algorithmus wirklich.
0.1ms=100μs (Mikrosekunden) an und nehmen somit den künftigen technischen Fortschritt vorweg. Denn alleine die I/O-Operationen auf den modernsten Datenträgern dauern derzeit (Stand Anfang 2019) ungefähr so lang. Unter dieser Annahme dauert eine Datenbank-Iteration 4 Sekunden lang und das hört sich erst mal nicht dramatisch an. Allerdings dürfen wir die übrigen 7499 Container 😀 nicht vergessen, die ebenfalls auf ihre Iterationen warten. Claro, nicht jeder Container wird es brauchen. Denn wenn ich mehrere nahezu identisch beladene rechne, weiß ich aus der ersten Iteration (durch das Punktesystem), was die geeigneten Stellplätze für die anderen sind. Dennoch müssen wir von dem berühmten worst case ausgehen, denn nur dieser beschreibt die immanente Komplexität eines Algorithmus wirklich.
Die Laufzeit fürs virtuelle Löschen unserer voll und heterogen beladenen „Sovereign Maersk“ beträgt demnach:
![]() und das sind immerhin 8 Stunden und 20 Minuten Laufzeit 😯
und das sind immerhin 8 Stunden und 20 Minuten Laufzeit 😯
An dieser Stelle wird sich der Leser möglicherweise fragen wie ist denn kommt, dass in Seehäfen wie Shanghai nicht alles buchstäblich stillsteht… Denn bei einer nunmehr 8-stündigen Beanspruchung ganzer Rechenzentren (Laufzeiten von 100 µs fürs ![]() sind nur mit Multinode-Computing möglich) müsste das ja über die meiste Zeit hinweg der Fall sein.
sind nur mit Multinode-Computing möglich) müsste das ja über die meiste Zeit hinweg der Fall sein.

Eine zu enge Lagerung von explosivem Gefahrgut hat zu einer regelrechten Kettenreaktion geführt. Die genaue Opferzahl kennt niemand. © bbc.com
Nun, die Antwort liegt in einer Optimierung des vorliegenden Algorithmus. Eine dieser Optimierungsoptionen haben wir bereits zuvor aufgezeigt: man pickt sich gleichartig bestückte Container heraus und errechnet für diese die geeigneten Stellplätze in nur einer Datenbank-Iteration (dies setzt freilich voraus, dass uns nicht der berühmt-berüchtigte worst case einholt). Eine andere Möglichkeit besteht darüber hinaus darin, bestimmte Bereiche des Containerhafens von der Zuteilung für eine zu löschende Ladung gänzlich auszuschließen und so die Zahl ![]() geringer zu halten.
geringer zu halten.
All das kann man natürlich machen – nur hört der Spaß spätestens dann auf, wenn jemand der Verlockung unterliegt und unmittelbar ans ![]() heran geht, indem er die Einzeleignungsprüfung aufweicht. Dass dieses „Optimierungspotenzial“ verlockend ist, liegt in der Natur der Sache. Zum einen kennen die Umsätze in den Seehäfen nur eine Richtung, nämlich nach oben, während der rechtliche Rahmen, etwa in Puncto Gefahrgut-Handling, Versicherung, Brand- und Strahlenschutz, Datenschutz etc. immer enger gezogen wird. Die Zeit arbeitet also gnadenlos gegen uns: das Optimierungspotenzial wird allmählich ausgeschöpft und der technische Fortschritt (Moorsches Gesetz) vermag dies nicht aufzufangen. Mit anderen Worten, wir laufen immer mehr in eine Zwickmühle hinein zwischen immer höheren Anforderungen auf der einen und nur begrezt vielen Möglichkeiten auf der anderen Seite. Die Fragestellung dieser AG lautet, kann uns der Quantencomputer aus dieser Zwickmühle heraushelfen?
heran geht, indem er die Einzeleignungsprüfung aufweicht. Dass dieses „Optimierungspotenzial“ verlockend ist, liegt in der Natur der Sache. Zum einen kennen die Umsätze in den Seehäfen nur eine Richtung, nämlich nach oben, während der rechtliche Rahmen, etwa in Puncto Gefahrgut-Handling, Versicherung, Brand- und Strahlenschutz, Datenschutz etc. immer enger gezogen wird. Die Zeit arbeitet also gnadenlos gegen uns: das Optimierungspotenzial wird allmählich ausgeschöpft und der technische Fortschritt (Moorsches Gesetz) vermag dies nicht aufzufangen. Mit anderen Worten, wir laufen immer mehr in eine Zwickmühle hinein zwischen immer höheren Anforderungen auf der einen und nur begrezt vielen Möglichkeiten auf der anderen Seite. Die Fragestellung dieser AG lautet, kann uns der Quantencomputer aus dieser Zwickmühle heraushelfen?

Verschränkung ist ein fürs Quantencomputing unabdingbarer Effekt.
Quelle © BBC.uk.com
Im Jahre 1996 stellte der Mathematiker Lov Grover einen Quantenalgorithmus vor, der in einer unsortierten Datenbank einen bestimmten Inhalt auffindet. Die Laufzeit ![]() , die ja für jedwede Datenbank-Iteration unumgänglich ist, konnte auf sensationelle
, die ja für jedwede Datenbank-Iteration unumgänglich ist, konnte auf sensationelle ![]() gesenkt werden 😯. Die Frage, die wir uns vorliegend stellen, lautet, kann der Grove-Algorithmus – freilich in einer für uns geeigneten Modifikation – unsere Stellplatz-Datenbank ebenfalls in
gesenkt werden 😯. Die Frage, die wir uns vorliegend stellen, lautet, kann der Grove-Algorithmus – freilich in einer für uns geeigneten Modifikation – unsere Stellplatz-Datenbank ebenfalls in ![]() iterieren? Und wenn ja, wäre damit unser Store Checkin Problem in einer nicht-kritischen Laufzeit gelöst?
iterieren? Und wenn ja, wäre damit unser Store Checkin Problem in einer nicht-kritischen Laufzeit gelöst?
Nun, letztere Frage kann man nur mit einem klaren Ja beantworten. Denn die Quadratwurzel aus 40.000 ergibt 200 und das mal 100 μs genommen bedeutet nur einen Sekundenbruchteil für eine volle Datenbank-Iteration. Bei dieser Laufzeit bräuchten wir keinerlei Kompromisse einzugehen – das virtuelle Löschen von unserer „Sovereign Maersk“ würde nur wenige Minuten dauern.
Die andere Frage, nämlich die nach der Korrespondenz des Grove-Algorithmus zur betreffenden Datenbank-Iteration, ist hingegen gleich mehrere Bits komplizierter. Es ist klar, dass sich die Stellplatz-Datenbank für den Grove-Algorithmus nahezu anbietet. Der Teufel 👿 dürfte aber im Detail stecken. Denn die alles entscheidende Frage lautet: Können wir die immanenten Eignungszahlen in Qubits abbilden?
Nach meinem Dafürhalten ist es der Fall, d.h. es existiert sehr wohl ein Quantenalgorithmus, der die vorliegend geforderte Iteration in ![]() verrichtet. Diese Vermutung ist vorläufig das einzige (Zwischen-) Resultat der vorliegenden AG, die somit – wie die AG übers QDD seinerzeit auch schon – mit einem an die Außenwelt gerichteten Ruf nach Hilfe zunächst endet.
verrichtet. Diese Vermutung ist vorläufig das einzige (Zwischen-) Resultat der vorliegenden AG, die somit – wie die AG übers QDD seinerzeit auch schon – mit einem an die Außenwelt gerichteten Ruf nach Hilfe zunächst endet. 
