Es handelt sich um eine Zusammenfassung der Veranstaltung, die am 13. Mai 2015 8:00-9:30 Uhr in der Gertrud-Luckner-Schule in Freiburg im Rahmen der Physik-Stunde stattfand.

Anwesend: …

Ergänzende Ausführungen, Vervollständigungen etc. wurden und werden peau à peau durch die Texteinschübe ➡ markiert.

 

Kernkraft als starke Wechselwirkung

.
Gedankenexperiment: Eine Wassermelone wird aus dem Fester im 2. Stock geworfen und zerplatzt am Boden.

Frage: Welche Urkräfte des Universums waren hier am Werke? Welche Wechselwirkungen haben die Wassermelone zerstört?

Nun, die Antwort, die sich einem zunächst aufdrängt – insbesondere wenn wir an „Urkräfte des Universums“ denken – lautet wohl “Gravitation” G. Denn offensichtlich war es hier die Erdanziehungskraft, durch die unsere Wassermelone erst Geschwindigkeit aufgenommen hatte und anschließend am Boden zerplatzte.

Die viel interessantere Frage in diesem Zusammenhang ist jedoch, was denn dafür gesorgt hat, dass die Wassermelone nicht bis zur Mitte der Erde durchgerutscht und dabei ganz geblieben ist? Was hat sie wirklich zerstört? Oder mit anderen Worten, welche Urkraft des Universums sogt dafür, dass wir überhaupt festen Boden unter den Füßen haben?

Diese Kraft (bzw. genauer: eine dieser Kräfte), die lange Zeit – neben der Gravitation – die einzig bekannte Wechselwirkung im Universum war, ist der Elektromagnetismus M ➡ Denn in der Tat hätten wir wohl kaum festen Boden unter den Füßen, wäre die Anziehungskraft zwischen den positiv aufgeladenen Protonen der Atomkerne und den sie umkreisenden negativ aufgeladenen Elektronen nicht bei dem Urknall mit entstanden. Wir hätten einen quasi plasmatischen Zustand der Materie unabhängig von der Temperatur und ob sich unter diesen Umständen Galaxien, Sterne und schließlich Planeten wie wir sie kennen gebildet hätten, ist wohl eher auszuschließen.

➡ Albert Einstein verbrachte die letzten Jahre seines Lebens mit der Suche nach einer Vereinigung beider Kräfte, also an der „Unification“ (G,M). Heute wissen wir, dass seine Versuche von vorne herein zum Scheitern verurteilt waren. Denn der klassische feldtheoretische Ansatz (ohne Quantenmechanik, die Einstein stets vehement ablehnte) dürfte wohl kaum das Graviton, dessen String auf zwei unterschiedlichen Branes füßt, jemals vollständig beschreiben – die später entdeckte starke und schwache Kernkraft schon gar nicht.
.
Einstein hat sich die Zähne ausgebissen bei seinen Feldgleichungen, wo insbesondere die diametral unterschiedlichen Stärken sowie Reichweiten beider Wechselwirkungen schier unüberwindlich waren. Auch das auf Teilchenmodellen beruhende Standardmodell musste von der Gravitation die Waffen strecken, obwohl die Vereinigung der übrigen drei Wechselwirkungen (M,W,S) sehr wohl gelang. Erst die Stringtheorie bringt die lang ersehnte „Unification“ (G,M,W,S) und liefert das lang postulierte Graviton.
.

Da gibt es aber mindestens noch eine Urkraft, die dafür sorgt, dass sich Galaxien, Sterne und schließlich Planeten haben bilden können. Diese mit Abstand stärkste Kraft im Universum ist der mächtige (Gluonen-) Klebstoff, der die Nukleonen der Atomkerne zusammen hält. Sie hat es also ermöglicht, dass aus der „Hadronen-Suppe“ nach dem Urknall andere Atomkerne entstanden sind, so dass wir – wie in dem Gedankenexperiment gesehen – festen Boden unter den Füßen haben. Die Rede ist von der starken Kernkraft S *)

________
*) Zu meinem Erstaunen nannte einer der Schüler auf die Ausgangsfrage hin zunächst eben die starke Kernkraft. 💡

.
Kern-Kraft?

.
Moment mal…Kernkraft? War da nicht etwas? Ist es nicht etwa das, was vor noch nicht allzu langer Zeit „Atomkraft“ genannt wurde? Ist es diese „Kern-Kraft“, die wir in Kernkraftwerken für uns nutzbar machen?

In der Tat führt diese historisch gewachsene Bezeichnung der starken Wechselwirkung zu einer Reihe von Missdeutungen insbesondere im Hinblick auf die Kernfusion bzw. herkömmliche Kernspaltung. So ist beispielsweise vor allem im Falle der Kernspaltung – manchmal etwas literarisch überhöht – vom „Entfesseln“ der starken Kernkraft die Rede, deren „Federwirkung“ etc. und ebenso vom „Freisetzen“ und Nutzung der nuklearen Bindungsenergie ➡

➡ Während die poetisch bis volkstümlich anmutenden (Ver-) Klärungen der starken Kernkraft eher den amateurhaften Kreisen vorbehalten bleiben, ist es mit der „Ausnutzung“ bzw. „Freisetzung“ der Bindungsenergie anders. Denn auch Fachleute liefern häufig die Erklärung für die Kernspaltung und die damit gewonnene Energie frei nach dem Motto, ein Atomkern werde gespalten wodurch die Bindungsenergie zwischen den Nukleonen, die sich nun der starken Kernkraft entzögen, freigesetzt werde.
.
Doch was ist so falsch an dieser Deutung? Nun, der grundlegende Denkfehler dabei ist von rein methodischer Natur; man könnte sagen, anders herum wird ein Schuh draus. Bindungsenergie ist nämlich nicht diejenige Energie, die man durchs Aufbrechen von Bindungen zwischen den Nukleonen (Kernspaltung) freisetzen kann, sondern vielmehr diejenige, die bei der Fusionierung einzelner Nukleonen des zusammengesetzten Kerns bereits freigesetzt worden ist! Mit anderen Worten, Bindungsenergie zwischen den Nukleonen eines Atomkerns ist diejenige Energie, die aufgewendet werden müsste, um einen Atomkern in seine einzelnen Nukleonen aufzuspalten.  Als Beispiel mag die hier bilanzierte Deuterium-Fusion zu Helium bzw. Tritium dienen.
.
Die Frage, die sich quasi automatisch daran anschließt, ist wohl: „Wie kommt es dann, dass wir bei der Spaltung von Uran oder Plutonium überhaupt Energie gewinnen? Das müsste doch dann energetisch gesehen ein reines Minus-Geschäft sein?“
.
Nun, der Knackpunkt liegt in der leicht zu übersehenden Tatsache, dass wir den Uran- oder Plutonium-Kern nicht in seine einzelnen Nukleonen aufspalten, sondern in zwei oder mehr durchaus zusammengesetzte Atomkerne. Hier lohnt sich der Blick auf die Bindungsenergie bezogen auf die Anzahl der Nukleonen im Atomkern. Beim reinen Wasserstoff ist die Bindungsenergie definitorisch gleich Null, während die Fusion zu Helium einen gewaltigen Sprung nach ober bedeutet. In der Tat ist dieser Effekt – die Zunahme der relativen Bildungsenergie (pro Nukleon) – bei den leichten Nukliden durchaus zu beobachten, aber dies nur bin in etwa Eisen ₂₆Fe. Ab da kehrt sich der Trend um. Von daher hat es keinen Sinn, etwa zwei Palladium-Kerne ₄₆Pd zu einem Uran-Kern ₉₂U zu fusionieren, weil wir hierfür Energie aufwenden müssten – und das nicht zu knapp. Um Umkehrschluss heißt es aber, dass wir beim Aufspalten von Uran in zwei Palladium-Kerne eben diese „nicht zu knappe“ Energie gewinnen werden! Genau darum geht es bei der kommerziellen Kernspaltung.
.

Zu all diesen Vorstellungen kann ich nur eine Empfehlung abgeben, nämlich „forget it“. Vergeßt insbesondere die „Bindungsenergie“ und operiert stattdessen mit dem sog. Massendefekt. In Wahrheit ist es wirklich so, dass beide kerntechnische Prozesse – Kernfusion wie Kernspaltung – obwohl definitorisch konträr zueinander verlaufend, eben diesen Massendefekt gleichermaßen hervorrufen (zumindest solange wir nicht auf die Idee kommen, schwere Nuklide zu fusionieren oder leichte zu spalten – s. obiger Einschub).

Masse verschwindet also spurlos (insbesondere ohne Abfall!) und dies kann lt. Einsteinscher Energie-Masse-Äquivalenz nur durch eine entsprechende Energiefreisetzung kompensiert werden:

Man könnte also salopp sagen, Kernfusion und Kernspaltung sind zwei unterschiedliche Methoden um Masse „auf den Kopf“ zu hauen. Die eine Methode ist besser, da praktisch abfallfrei und mit einer nur mäßigen Neutronenstrahlung, die zudem noch auf die echten Betriebszeiten beschränkt bleibt (kein „strahlender“ Abfall), während die andere Methode, die Kernspaltung nämlich, durchaus mit einigen nicht sehr angenehmen Nebenwirkungen verbunden ist. Aber beide zielen auf den gleichen Effekt ab, nämlich den Massendefekt. ➡

➡ Dieser Massendefekt ist es auch, was die Kernenergie so attraktiv und ertragreich macht. Nehmen wir z.B. die Kernfusion. Man stelle sich vor, auf Kosten von ein paar Gramm Wasserstoff pro Tag (zzgl. ein par Kilo Helium quasi als „Abfall“), hätten wir eine (Um-) Welt, in der kaum ein Schornstein und kaum ein Auspuffrohr rauchen würde, ohne Windturbinen, Staudämme, Bioreaktoren etc. Dass die Schadstoffbelastung unter diesen Umständen dramatisch sinken und die Qualität der Umwelt dramatisch steigen würde, ist wohl offensichtlich.
.

Einziger Haken bei der Kernfusion (als Methode zur Energiegewinnung): sie ist schlicht (noch) nicht da. Die Kernspaltung hingegen ist sehr wohl Realität und bildet die Basis für alle derzeit in Betrieb befindlichen Kernkraftwerke. Demzufolge konzentrieren wir uns im nächsten Abschnitt ausschließlich auf die (herkömmliche ➡ ) Kernspaltung.

➡ Unter der herkömmlichen (oder auch „normalen“) Kernspaltung bzw. Kernkraft verstehen wir hier stets Prozesse bzw. technische Einrichtungen, die primär auf Spaltung von geeigneten Atomkernen mit Hilfe von langsamen (auch „thermischen“) Neutronen abzielen. Damit sind weder „schnelle“ Neutronen noch Schwerwasser-Reaktoren gemeint.

.
Kernmutationen. Periodensystem der Elemente

.
Beim genaueren Blick auf die minoren Actinoide (unterhalb von Americium) im Periodensystem fällt einem zunächst eine kleine Regemäßigkeit auf und zwar: Während Actinium, Proactinium und Neptunium kaum im Zusammenhang mit herkömmlicher Kerntechnik genannt werden, ist es beim Thorium und erst recht beim Uran oder Plutonium sehr wohl der Fall. Betrachten wir die Ordnungszahlen dieser minoren Actinide, so stellen wir fest, dass diese bei ₈₉Ac, ₉₁Pa, ₉₃Np ungerade sind, während es bei ₉₀Th, ₉₂U, ₉₄Pu anders herum ist. Ein Zufall?

.

 

.
Nun wissen wir nicht zuletzt aus dem Studium des obigen Periodensystems, dass einzig und alleine die Ordnungszahl ein chemisches Element zu dem macht, was es ist. So machen exakt die 8 Protonen im Sauerstoff-Atomkern zu demjenigen Gas, mit dem sich fantastisch atmen lässt, während bloß ein Proton weniger die herrliche Luft zum Stickstoffgift machen würde. Jedoch bei näherer, etwas mehr kerntechnisch fundierter Betrachtung, ist es nicht so sehr die Anzahl der Protonen, wie deren geometrische Anordnung (freilich resultiert diese letztendlich aus der Anzahl, also hier schließt sich der Kreis so oder so).

Was ich damit sagen will, ist, dass es für die Eigenschaften eines chemischen Elements bzw. in unserem Beispiel eines minoren Actinids, sehr wohl interessant ist, ob es zu jedem Proton (und Neutron!) ein Gegenüber gibt. Bei den „geraden“ Elementen ist es der Fall, bei den ungeraden nicht. So gesehen ist es nicht allzu verwunderlich, dass Neptunium z.B. nicht sehr „stabil“ ist. Es neigt einerseits zum klassischen Zerfall, anderseits zum sog. β^–-Zerfall, infolge dessen es zu Plutonium transmutiert (dazu später mehr). Es bleibt uns also nicht allzu lange „erhalten“.

Gleichen Effekt können wir aber auch bei den Neutronen beobachten. Nun beeinflussen Neutronen den Charakter eines Atomkerns längst nicht so radikal, wie es die Protonen tun (indem sie ja die Identität eines Elements eindeutig bestimmen), aber auch deren Anzahl im Atomkern ist sehr wohl von Bedeutung: wir sprechen bei verschiedenen Massenzahlen (also Nukleonenzahlen) von sog. Isotopen. Die bekanntesten auch in der freien Wildbahn vorkommenden Uran-Isotope sind ²³⁵U und ²³⁸U. Beide unterscheidet lediglich die Anzahl der Neutronen im Atomkern – die der Protonen bleibt unverändert bei 92. Insofern ist die Schreibweise „₉₂U“ eigentlich eine klassische Tautologie! 😀

Beide Isotope unterscheidet aber nicht nur die Anzahl der Neutronen im Kern, sondern auch und insbesondere deren Parität. So wie bereits bei der Ordnungszahl der minoren Actinide beobachtet, hat das 238’er Uran zu jedem Nukleon ein Pendant, das 235’er jedoch nicht. So verwundert es nicht, dass das letztere weniger stabil (aber sehr wohl leichter spaltbar!) ist und demzufolge in dem sog. Natururan ➡ viel seltener vorkommen dürfte. Und in der Tat beträgt dessen Anteil im Natururan lediglich 0.7% – zu wenig, um ein thermisches Kernkraftwerk zu betreiben. Um auf die benötigten 3-5% zu kommen, müssen wir den Anteil entsprechend erhöhen, also das Natururan „anreichern“. Zu den bekanntesten Anreicherungsmethoden zählt der Einsatz von Zentrifugen (siehe etwa gegenwärtiges iranisches Atomprogramm). Logisch, denn beide Isotope unterscheiden sich in deren Gewicht: der Unterschied beträgt ca. 3 Neutronen.

➡ Ein weit verbreiteter Irrglaube suggeriert, dass Uran erstens bald „alle“ ist und zweitens irgendwie auf die Kernkraft zurückgeht. In Wahrheit gehört Uran zu den am meisten verbreiteten Elementen in der Erdkruste und in den Gewässern. Alleine in den Weltmeeren sind sage und schreibe 4 Milliarden Tonnen Uran verteilt, davon ca. eine Million Tonnen von dem „Atomwaffen-fähigen“ ²³⁵U.
.

Kernspaltung

.
Stellen wir uns vor, ein Neutron kommt angeflogen und trifft auf eines der Pellets ➡ , mit denen die Brennelemente reichlich bestückt sind. Stellen wir uns des weiteren vor, unsere Pellets bestehen aus reinem (und angereicherten) Uranoxid. Unser Neutron wird also mit einer ziemlichen Wahrscheinlichkeit auf ²³⁸U-Kerne treffen, mit einer etwas geringeren Wahrscheinlichkeit auf die des ²³⁵U. Betrachten wir zunächst den letzteren Fall.

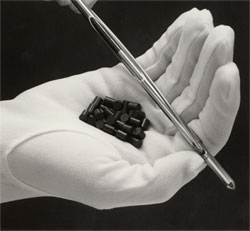➡ Pellets aus Uran-Plutonium-Mischoxid (sog. MOX). Der Handschuh schützt nur indirekt die Hand: Schweiß tut den Pellets gar nicht gut (dazu später mehr). Nebenan ein Brennstab mit Ummantelung aus Zirkonium, einem Refraktärmetall, das in bestimmten Temperaturbereichen gerne Sauerstoff aus ggf. vorhandenem Wasserdampf an sich zieht. Der frei gewordene Wasserstoff führte im März 2011 zu den Knallgasexplosionen in den Reaktorgebäuden des japanischen Kernkraftwerkes Fukushima Daiichi.
.

Was wird wohl passieren, wenn ein Neutron auf einen Kern des leicht spaltbaren und „Atomwaffen-fähigen“ Uran zurast? Zunächst eine andere Frage: Was wissen wir über dieses Neutron? Die Antwort ist, wir wissen so ziemlich alles. Wir kennen seine Masse, Ladung, korrespondierende Quarks oder Strings – kurz, so ziemlich alles wissen wir über dieses Teilchen und zwar aus dem Grund, dass Neutronen unabhängig von deren Herkunft schlicht Neutronen bleiben. Dabei ist es unerheblich, ob das Neutron aus einem Urankern-Zerfall im Brennelement eines Kernkraftwerks oder einem natürlichen Kalium-Zerfall im Blatt Biosalat  stammt – es gibt schlicht keinen wesenhaften Unterschied.

Einziger Parameter bzw. Eigenschaft, die von Bedeutung ist für den Ausgang der Begegnung mit dem Atomkern, ist in der Tat die Geschwindigkeit. Da die Herkunft des Neutrons mit hoher Wahrscheinlichkeit der Zerfall eines Uran-Kerns ist, dürfen wir voraussetzen, dass die Geschwindigkeit des Neutrons relativ hoch ist; man spricht von „schnellen“ bzw. „hochenergetischen“ Neutronen, da die hohe Geschwindigkeit eine hohe kinetische Energie impliziert: .

Was passiert also beim Aufprall eines solchen schnellen Neutrons auf einen ²³⁵U-Atomkern? Mit einer ziemlich hohen Wahrscheinlichkeit passiert… gar nichts. Denn ein schnelles Neutron ist eben zu schnell, als dass es beim ²³⁵U „andocken“ kann. Es rast daran vorbei wie ein Komet an einem Himmelskörper, dessen Fluchtgeschwindigkeit weit unter der des Kometen liegt. Und selbst wenn das Neutron den Kern trifft, ist es nicht unwahrscheinlich, dass es durch diesen Kern glatt „hindurchschießt“. Also, außer Spesen nichts gewesen. Das Neutron fliegt weiter und wir haben nichts davon.

Nun stellen wir uns vor, die Brennelemente (also auch Pellets) sind ins Wasser getaucht und unser Neutron muss demzufolge den Weg von einem Pellet ins andere durchs Wasser nehmen. Hier passiert etwas, was man auch „Moderation“ nennt. Das Neutron verliert an Energie und somit Geschwindigkeit. Diese geminderte Geschwindigkeit reicht aber nicht mehr aus, um am ²³⁵U-Kern vorbeizufliegen. Ein solches „thermisches“ ➡ Neutron wird eingefangen.

➡ das Attribut „thermisch“ geht auf die korrespondierende elektromagnetische Welle zurück, die im Bereich der Wärmestrahlung angesiedelt ist (vgl. Welle-Teilchen-Dualismus)
.

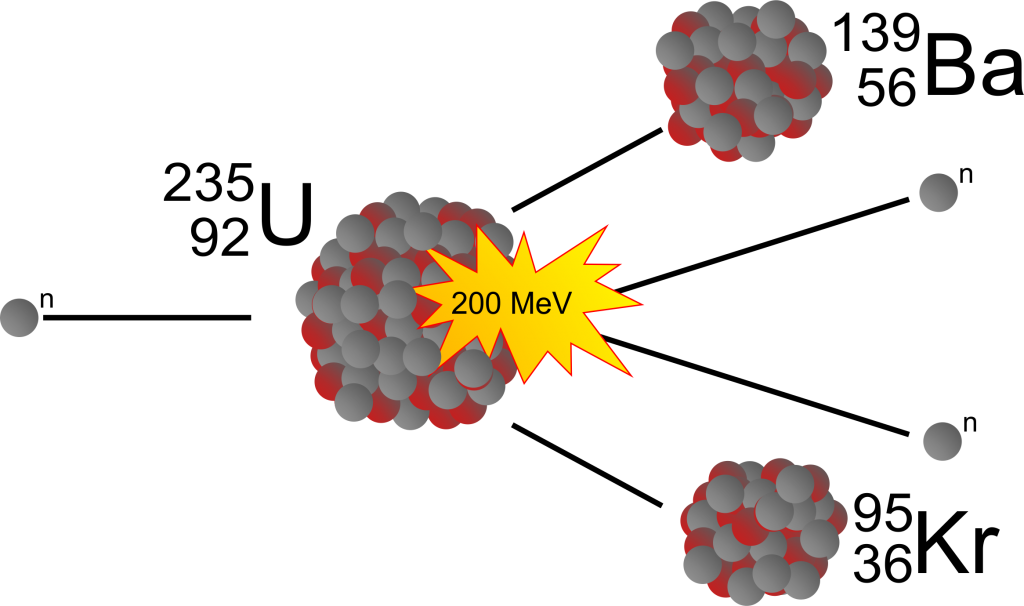Was also zunächst logischerweise passiert, ist die Aufnahme des 236’ten Nukleons in den ²³⁵U-Kern, also gewissermaßen eine Mutation zu einem anderen Isotop, nämlich dem ²³⁶U. Wir erinnern uns an die Regel mit den geraden und ungeraden Nukliden. Demnach müsste dieses Isotop eher stabil sein und nicht mehr so einfach spaltbar, jedenfalls für die thermischen Neutronen nicht. Das stimmt auch soweit, bis auf die Stabilität im Sinne der Radioaktivität. Denn diese ist beim ²³⁶U weitaus höher als beim ²³⁸U – ansonsten aber ist dieses Isotop zumindest aus der Sicht eines herkömmlichen Leichtwasserreaktors in der Tat „Müll“. Also, irgendwie sind wir von Pech verfolgt. Schon wieder außer Spesen nichts gewesen?

Nein, so schlimm ist es nicht. Denn die Bildung des 236’er Uran ist eher selten: nur in etwa jedes fünfte Eindringen eines Neutrons in den ²³⁵U-Kern endet so. In den übrigen 80% der Fälle kommt es dann doch (endlich!) zur Spaltung des ²³⁵U-Atomkerns in zwei (seltener in drei) Zerfallskerne, die definitorisch leichter sind und uns den oben beschriebenen satten Energiegewinn bescheren. Mit ein bisschen Glück kommen dabei zwei stabile Nuklide heraus, die sogar wertvolle Stoffe sein können, aber dies passiert leider eher selten; dazu gleich mehr.

Frage aus der Runde: Wenn ich 70% von ²³⁵U hätte, könnte ich dann mehr Energie erzeugen?

Antwort: Die Energieausbeute aus einer ²³⁵U-Spaltung bleibt gleich, allerdings wäre die Anzahl der Spaltungen und der damit freigesetzten Neutronen auf kleinstem Raum so enorm, dass es zu einer atomaren Explosion käme.

Nukleares Brüten

.
Nun haben wir bislang die Begegnung eines thermischen Neutrons mit dem 235’er Uran diskutiert, obwohl dieses Isotop nur mit 3-5% in den herkömmlichen Brennelementen vertreten ist. Es ist daher – zumindest rein statistisch gesehen – wahrscheinlicher, auf einen ²³⁸U-Kern zu treffen. Was dann passiert wollen wir uns nun anschauen:

 

.
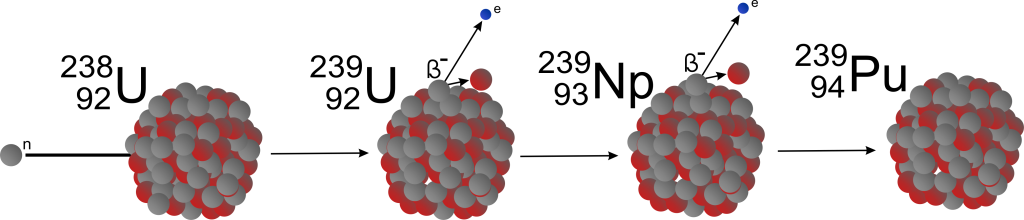
Nach dem Eindringen in einen 238’er-Kern erhöht sich zunächst mal – logischerweise – die Nukleonenzahl und zwar auf 239. Das Resultat ist ein uns bis dato unbekanntes Isotop ²³⁹U. Laut bisher diskutierter Nukleonen-Arithmetik dürfte dieses Isotop bei einer ungeraden Nukleonenzahl nicht sehr stabil sein – müsste also demnach relativ schnell zerfallen. Allerdings zeigt sich hier eine andere Art der Instabilität, nämlich die Neigung nicht zum „klassischen“ Zerfall (hin zu „kleineren“ Nukliden) sondern zum sog. β^–-Zerfall. Dieser beruht auf dem Zerfall eines Neutrons in ein Proton und Elektron, wobei noch ein winzig kleines Teilchen, nämlich das Neutrino, mit emittiert wird.

Für den betreffenden ²³⁹U-Atomkern heißt es, dass ein Neutron zum Proton quasi mutiert ist, während die Gesamtzahl aller Nukleonen im Kern unverändert 239 beträgt. Da wir aber aus dem Studium des Periodensystems wissen, dass es die Protonenzahl ist, die ein Element ausmacht, sehen wir sofort, dass bei dieser „Mutation“ Uran zu Neptunium ²³⁹Np geworden ist (da Neptunium das unmittelbar nächste Element im Periodensystem liegt und ein erstes sog. Transuran ist, spricht man hier von der nuklearen „Transmutation“).

Soweit so gut. Über Neptunium wissen wir jedoch, dass es uns nicht allzu lange erhalten bleibt. Und in der Tat lässt der nächste β^–-Zerfall nicht lange auf sich warten: das Resultat ist nun das Plutonium ²³⁹Pu. Dieses Isotop ähnelt gerade wegen seiner ungeraden Nukleonenzahl sowie der geraden Ordnungszahl sehr stark dem ²³⁵U. Es ist für thermische Neutronen relativ empfänglich und von daher ein durchaus brauchbarer Brennstoff. Was wir also hier beobachten, ist ein seltsamer Prozess, der aus dem per se nicht-spaltbaren ²³⁸U ein sehr wohl spaltbares ²³⁹Pu „erbrütet“.

Inhärente Sicherheit

.
Das Verhalten der spaltbaren Isotope ²³⁵U oder ²³⁹Pu gegenüber den thermischen Neutronen ist zumindest paradox. Denn die Antwort auf die Frage, wie ich Brennelemente eines herkömmlichen Kernkraftwerkes zum Glühen bringen kann, lautet schlicht, „indem ich diese ins Wasser tauche“.

Doch dieses Paradoxon bringt eine sehr angenehme Eigenschaft mit sich, nämlich eine gewissermaßen „einprogrammierte“ – man könnte auch sagen „innewohnende“ oder „inhärente“ – Bremsfunktion bezogen auf die Reaktivität. Denn stellen wir uns vor, der Druckbehälter eines Druckwasserreaktors schlägt leck und der Druck sackt ab. Das hat dann aber zur Folge, dass sich um die Brennelemente herum – ähnlich wie bei einem Tauchsieder – Luftblasen bilden. Luftblasen sind aber nicht Wasser, also nimmt die Neutronenmoderation und somit die Reaktivität entsprechend ab. Die Brennelemente „heizen“ dann weniger stark.

Hier liegt ein gewisser Vorteil eines Druckwasserreaktors gegenüber einem Siedewasserreaktor klar auf der Hand. Denn beim letzteren sind Luftblasen um die Brennelemente herum der normale Betriebszustand, während es beim ersteren eine Betriebsstörung ist, die erstens als solche erkannt werden kann und zweitens zur Aktivierung der inhärenten Bremsfunktion führt.

Es gibt aber auch andere Parameter, an die man eine solch inhärente Bremsfunktion – oder wenn Ihr so wollt – Selbstregelungsfunktion festmachen kann, so dass auch ein Siedewasserreaktor hiervon profitieren kann – etwa die Temperatur. Denn wie wir alle gesehen haben, gingen die meisten schweren Failouts von Kernkraftwerken mit steigender Temperatur einher. Die Frage ➡ ist, ob sich ein Mechanismus implementieren lässt, der bei steigender Temperatur die Reaktivität drosselt und zwar nicht durch Aktivierung von externen Systemen (z.B. aktiven Kühlern), die für sich genommen ausfallen können, sondern quasi von alleine, den natürlichen Gesetzmäßigkeiten folgend.

➡ Von einem sehr aufmerksamen Zuhörer kam an dieser Stelle die Frage, wie eine solch inhärente Selbstregelung bei den nicht-moderierten Neutronen zu realisieren sei? 💡 (Zuvor war in einer kurzen Zwischenbemerkung angedeutet worden, dass nur die schnellen Neutronen die „geraden“ Nuklide spalten können).
.

An dieser Stelle war die Veranstaltung leider zu Ende. Fragen der inhärenten Sicherheit bei schnellen Brennern bzw. -Brütern, Grundkonzepte aus der sog. Generation 4 der Kernkraftwerke sowie die Möglichkeiten der Atommüll-Verbrennung werden demnächst hier auf „AG Energetik“ erörtert werden. Eine mit der vorliegenden vergleichbare Veranstaltung ist zur Stunde noch nicht anberaumt worden.

 
https://www.facebook.com/rainer.stawarz/posts/1608374372711778