Sättigung bei den „Erneuerbaren“ Energien. Der χ- (Chi-) Effekt

»

Untersucht wird das dynamische Verhalten von Erntefaktoren (EROI) „Erneuerbarer“ Energien, insbesondere Wind- und Solarkraft, hinsichtlich installierter Leistung. . Das Fazit der AG ist wirklich niederschmetternd für die Windkraft- und Solarindustrie – ja, man kann mit Fug und Recht von einem Super-GAU sprechen. Denn wie zuvor vermutet, hat sich der Negativtrend bei den χ_u-Koeffizienten auch in den Jahren 2019-2021 fortgesetzt. Folglich wird bereits der ungepufferte EROI mit zunehmendem Ausbau der „EE“ immer schlechter und zwar allem technischen und technologischen Fortschritt zum Trotz! Berücksichtigt man ferner noch die Pufferung (was eine anderweitige AG in ihrer Fortsetzung untersuchen wird), dürfte der Nachweis für eine „EE-Sättigung“ endgültig erbracht sein! Ein weiterer Zubau von Wind- oder Solar würde dann nahezu vollständig verpuffen und das viel apostrophierte Ziel „100% EE“ als physikalisch unerreichbar ausweisen.	^T_E ^L_E ^G_R ^A_M

Motivation. Hintergründe

Wind-und-Solar-2011-bis-2015 — Man sieht allenfalls minimale Zunahmen bei den Peaks – und das trotz einer beinahe Verdopplung (!) der installierten Leistung.
© Rolf Schuster (@science-skeptical.de)

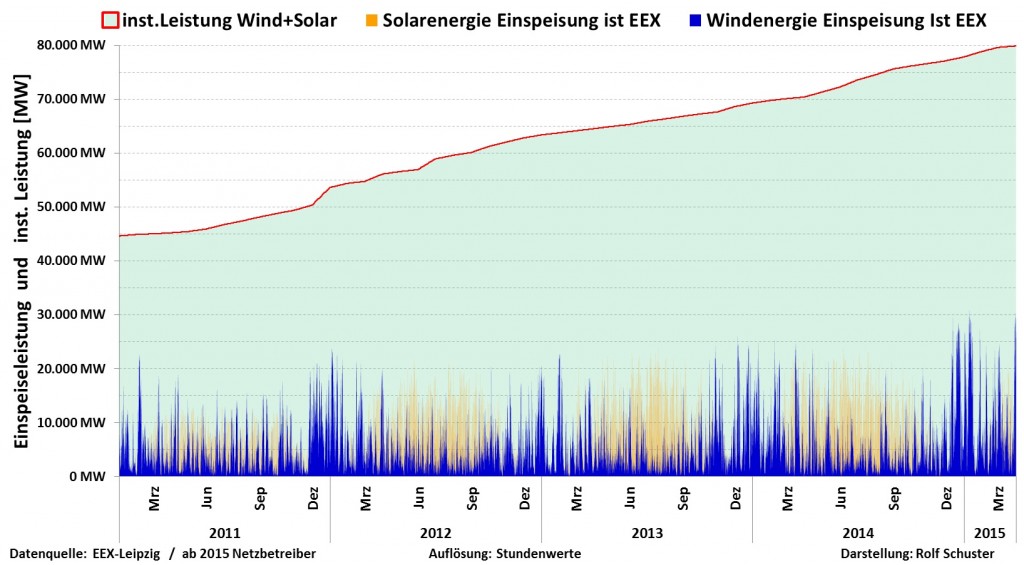
Am 15. September 2015 schloss die AG „Energieeffizienz von Windkraftanlagen“ mit der für so manche (aber eben nur für manche 😉) überraschenden Erkenntnis, nämlich, dass der energetische Gewinn aus Windkraftanlagen mit der installierten Leistung derselben nicht Schritt hält. Der im Laufe dieser AG geprägte Terminus hierfür, der meinen Namen mitführte, gelangte seinerzeit – aus welchen Gründen und auf welchen Umwegen auch immer – zu Google und so reagiert die Suchmaschine bis heute auf den „Effekt“, den ich hier nicht noch einmal explizit nennen möchte. Zu schreiben, es hieße nicht „St…-Effekt“ sondern „Betzscher Effekt“, erhöht ja bekanntlich nicht nur die Rankings vom letzteren…

In der Tat sprach ich persönlich eher vom „Betzschen Effekt“ und untermauerte in der AG den beobachteten Effekt mit dem Betzschen Gesetz, das die Energieausbeute aus einer WKA von der 3’er Potenz der Windgeschwindigkeit abhängig macht.

Allerdings hatte ich von Anfang an Zweifel daran eingeräumt, ob es mit dem Betzschen Effekt alleine wirklich getan sei. Das obige Diagramm jedenfalls scheint da kaum einen Unterschied zur Sonne zu suggerieren, bei der es diese „Betzsche“ 3’er Potenz bekanntlich gar nicht gibt.

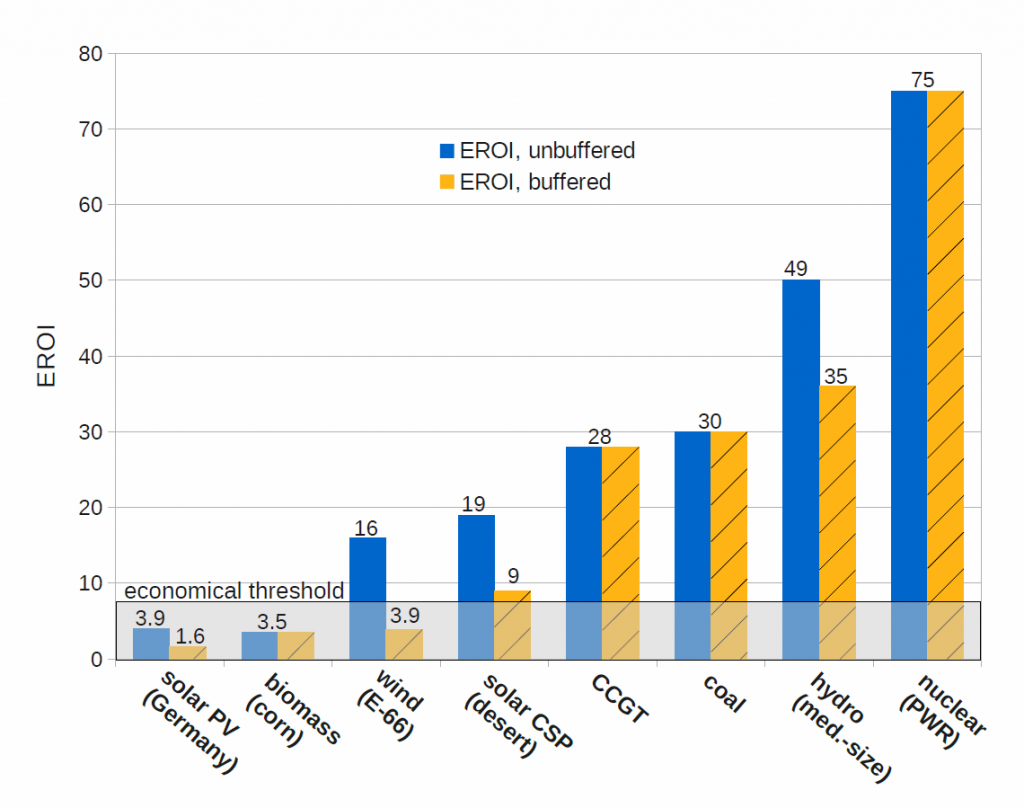
EROI-of-Solar-Wind-Nuclear-Coal-Natural-Gas-Hydro — Das Diagramm entstand in der 1. Dekade dieses Jahrhunderts.
Die Erntefaktoren (EROI) dürften inzwischen obsolet sein.
Quelle © Institut für Festkörper-Kernphysik

So kündigte ich an, baldmöglichst zu untersuchen, ob nicht mehr dahinter steckt. Nun ist es mit dem „baldmöglichst“ so eine Sache gewesen… 😳. Denn trotz Eurer eindringlicher Fragen, wie es denn wohl bei PV aussehen würde o.ä., wandte ich mich zunächst anderen AG’s zu, führte die Sparte „Quantencomputing“ ein etc. Aber der wahre Grund war der, dass ich die (vermutete) Entwicklung abwarten wollte. Und meine Vermutung, die von der vorliegenden AG untersucht werden wird, ist schlicht die folgende:

💡 Die Abflachung der Energieernte – somit Verschlechterung des (gepufferten) EROI – nimmt mit zunehmender EE-Dichte zu. Wir nennen es „κ- (Kappa)“-Effekt ➡

Gerade diese Entwicklung war in den letzten Jahren mit Händen zu greifen. Während man noch zu Anfang des Jahrzehnts der Windkraft einen (gepufferten) EROI von immerhin 4 attestieren hat können, kam die AG „Erntefaktoren der Nord- und Ostsee Offshoreparks“ selbst bei Vorzeigeanlagen à la „Amrumbank West“ bzw. „Alpha-Ventus“ sowie bei einer äußerst wohlwollenden Berechnung nicht über 3.76 hinaus. Bei PV wird’s indes komplett absurd: Denn waren es früher noch 1.6 – errechneten neuerdings Schweizer Forscher gerade mal eine knappe 1 👿

➡ Mit κ- (Kappa) wurde bereits im Teil 1 der AG „Erntefaktoren der Nord- und Ostsee Offshoreparks“ der dort postulierte „Pufferungskoeffizient“ bezeichnet und als das Verhältnis vom ungepufferten zum gepufferten EROI 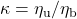$\kappa=\eta_\text{u}/\eta_\text{b}$ verstanden.
.

Grundlegende Konzepte. Aufgabenstellung

.
Unter dem „Pufferungskoeffizienten“, der seinerzeit im Teil 1 der AG „Erntefaktoren der Nord- und Ostsee Offshoreparks“ eingeführt worden ist, verstehen wir den Quotienten des ungepuffertem zu dem gepufferten („buffered“) EROI:

$\kappa_\text{e}=\frac{\eta_\text{u}}{\eta_\text{b}}$ ; der Index „e“ steht für eROI-basiert.

Nach den einzelnen Energiearten lässt er sich demnach folgendermaßen auflösen:

$\kappa_\text{e}=\frac{E_\vartriangleleft+E_\text{b}}{E_\vartriangleleft}=1+\frac{E_\text{b}}{E_\vartriangleleft}$ wo $\textstyle{E_\vartriangleleft}$ kfür die aufgewendete Energie, also energetische „Unkosten“ steht und zwar ohne Pufferung.

Dass sich die geerntete Energie $\textstyle{E_\vartriangleright}$ „weggekürzt“ hat, überrascht dabei nicht sonderlich: $\textstyle\kappa_\text{e}$ beschreibt die Pufferung – nicht die Energiegewinnung.

Demnach ist $\textstyle\kappa_\text{e}$ eine Zahl, die bei grundlastfähigen Energien definitorisch 1 beträgt und bei den EE’s eben größer 1 ist. Zu Zeiten vom obigen Diagramm betrug $\textstyle\kappa_\text{e}$ für Windkraft etwa 4 und für PV knapp unter 2. Ob und in welcher Richtung sich diese Koeffizienten inzwischen verändert haben könnten, sollte eben die vorliegende AG untersuchen.

Als nächstes müssen wir uns genau plausibel machen, was mit der Pufferungsenergie $\textstyle{E_\text{b}}$ gemeint ist. Es handelt sich nämlich um diejenige Energie, die für die Pufferung „extra“ bereitgestellt werden muss. Energie (bzw. technische Vorrichtungen), die so oder so da ist und nicht speziell durch die Pufferung erzwungen wird, zählt hingegen nicht zu $\textstyle{E_\text{b}}$ dazu.

Beispiele:

OlivierMaire_Swisswinds_f2ec60f334 — Eine Idylle, die hoffentlich Fotomontage bleiben wird.
© Olivier Maire. Swisswinds

1) Das Stromnetz selbst hat eine (wenn auch eine äußerst geringe) Speicherkapazität, die zur Pufferung von EE’s genutzt wird. Die Aufwendungen, die damit verbunden sind, können jedoch nicht aufs $\textstyle{E_\text{b}}$ -Konto gerechnet werden, da das Stromnetz „so oder so“ da ist. Muss es hingegen ausgebaut werden, um z.B. mit zunehmender Menge an volatilem Strom fertig zu werden, zählen diese Aufwendungen, etwa die graue Energie, ganz klar zu $\textstyle{E_\text{b}}$ dazu;

2) Ein Wasserkraftwerk, das z.B. einen kleinen Windpark intermittierend puffert, hat einen begrenzten Wasserzufluss, also erzwingt der Windpark selbst keinen „suboptimalen“ (weil gedrosselten) Betrieb, wie dies z.B. beim Kohlekraftwerk, das auf 60% der Nominalleistung fährt, der Fall ist. Verluste an den Wasserturbinen entstehen so oder so, früher oder später. Dies funktioniert freilich nur so lange, bis der Stausee voll- oder leerläuft. 😳

Was können wir aus diesen Beispielen lernen?

Solar-2011-bis-2015 — Den Betzschen Effekt gibt es bei Solarenergie von Physik wegen nicht – dennoch ähnelt der Verlauf jenem der Windkraft stark.
© Rolf Schuster (@science-skeptical.de)

Zunächst, dass $\textstyle\kappa_\text{e}$ offensichtlich nicht konstant ist. Bis zu einem gewissen Grade kann es sogar für EE’s 1 (oder nahe 1) betragen, steigt dann aber offensichtlich an. Ferner können wir schlussfolgern, dass das System – sowohl global (Beispiel 1)) als auch lokal (Beispiel 2)) – eine natürliche (wenn auch sehr begrenzte!) Pufferungskapazität besitzt. Wird diese überbeansprucht, steigt $\textstyle\kappa_\text{e}$ entsprechend an.

Womit aber hängt der Anstieg von $\textstyle\kappa_\text{e}$ zusammen? Wann tritt die „Überbeanspruchung“ der Pufferungskapazität ein?

Nun, es hängt alles offensichtlich mit der Menge an volatilem Strom zusammen. Denn bei andauernder Dunkelflaute läuft uns der Stausee schneller leer, wenn das Wasserkraftwerk für 100 stillstehende Windräder aufkommen muss, wie wenn es nur 10 sind. Also liegt die Vermutung nahe, dass ein Zusammenhang mit der installierten Leistung besteht.

Allerdings haben wir bereits anhand von den obigen Beispielen gesehen, wie schwierig es im Einzelfall sein kann, die Pufferungsverluste $\textstyle{E_\text{b}}$ und andere Unkosten $\textstyle{E_\vartriangleleft}$ auseinander zu halten. Dieser Umstand bietet insbesondere der EE-Industrie und deren Apologeten reichlich Angriffsfläche um das $\textstyle\kappa_\text{e}$ und damit die EROI’s schön zu rechnen. Die Grundidee der vorliegenden AG besteht jedoch darin, nicht die Koeffizienten selbst, sondern vielmehr deren Veränderungen im Laufe der Zeit, also gewissermaßen deren Fluxionen ➡, zu untersuchen. Mit anderen Worten, wir schenken Euch die ganze Pufferung und die ganzen EROI’s; die mögen im Gottes Namen noch so günstig sein. Tun sie sich aber kontinuierlich verschlechtern, gibt es früher oder später einen Punkt, ab dem ein weiterer Ausbau der EE’s effektiv nichts mehr nutzt; ein Sättigungspunkt tritt ein.

➡ Unter „Fluxionen“ verstehen wir – nach guter alter Newton-Manier 😉 – schlicht Differential- bzw. Differenzenquotienten, also 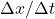$\textstyle{\Delta{x}/\Delta{t}}$ bzw. $\textstyle{dx/dt}$ .
.

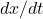Apropos Zeitpunkt und (Zeit-) Fluxionen. Es ist für unsere Betrachtungen wenig interessant, wie sich die einzelnen Koeffizienten z.B. von Jahr zu Jahr entwickeln. Denn nicht der Zeitfaktor ist entscheidend, sondern vielmehr sind’s die Veränderungen von Rahmenbedingungen, die in dem betrachteten Zeitraum eingetreten sind. Im Laufe eines Jahres beispielsweise kann ein technischer und technologischer Fortschritt stattgefunden haben, die Systeme können effizienter geworden sein etc. – was sich nur positiv auf $\textstyle\kappa_\text{e}$ und die EROI’s ausgewirkt haben kann. Allerdings kann im gleichen Zeitraum noch etwas anderes eingetreten sein, nämlich der Zubau an EE’s und somit Zunahme an installierter Leistung. Schön und gut, aber bedeutet der Zubau an EE’s zwangsläufig einen adäquaten Zuwachs bei geernteter Energie? Oder bessern sich gar $\textstyle\kappa_\text{e}$ und somit der EROI’s?

Nun, beim Letzteren haben wir doch erhebliche Zweifel – denken wir an die bereits erwähnte AG „Energieeffizienz von Windkraftanlagen“ bzw. an die obigen Diagramme von „science-skeptical.de“. Es sieht eben nicht gerade danach aus, als sollte etwa eine Verdopplung der Windkraft automatisch eine Verdopplung der gewonnenen Windenergie nach sich ziehen. Doch wenn dem so ist, in welchem Verhältnis steht dann die (relative) Zunahme der effektiv „geernteten“ Energie zum Ausbau derselben? Wir definieren einen modifizierten Koeffizienten, den wir im Gegensatz zu den obigen Überlegungen nicht mit $\textstyle\kappa_\text{.}$ sondern mit $\textstyle\chi_\text{.}$ bezeichnen wollen, um Verwechslungen vorzubeugen:

$\chi_\text{u}+1:=\frac{E^{(\Delta{t})}_\vartriangleright/E_\vartriangleright}{P^{(\Delta{t})}_\text{i}/P_\text{i}}$ ; dabei steht der Index „u“ für unbuffered; dazu gleich mehr.

Da haben wir uns einen etwas kuriosen anmutenden Koeffizienten zusammengestellt. Denn was wir da ins Verhältnis zueinander setzen, ist einerseits die in einem Zeitraum Δt effektiv produzierte Energie und anderseits die vorhandene installierte Leistung, wobei in beiden Fällen das relative Wachstum hergenommen wird.

Doch während die „geerntete“ Energie eine integrale Größe ist, ist die installierte Leistung ein punktueller Wert. Betrachten wir den Zuwachs zwischen dem Anfang und dem Ende des betrachteten Zeitraums (z.B. Jahreszeitraums), so stellen wir fest, dass wir nicht genau wissen, wie dieser Zuwachs zeitlich verteilt war. Hat er im Wesentlichen am Frühjahr stattgefunden, so ist der Einfluss auf die Energieernte wesentlich größer, als wenn er erst gegen Jahresende stattgefunden hätte. Um diesem Fehler zu entgehen, müssten wir den betrachteten Zeitraum verkürzen… aber da laufen wir voll in die saisonalen Schwankungen hinein und unser $\chi_\text{u}$ wird entsprechend ungenauer… ➡

➡ Wer mag, darf darin eine Parallele zur Heisenbergschen Unschärferelation sehen. Je genauer wir etwas verorten, auch zeitlich, umso unschärfer wird dessen Impuls und umgekehrt.
.

Demzufolge müssen wir – um den saisonalen Schwankungen zu entgehen – den betrachteten Zeitraum auf ein Jahr festsetzen („+365“), wohl wissend, dass unser $\chi_\text{u}$ mit einem intrinsischen Fehler behaftet ist, der mit zeitlich ungleichmäßiger Verteilung des Zubaus an EE’s übers Jahr betrachtet zusammenhängt:

$\chi_\text{u}=\frac{E^{(+365)}_\vartriangleright/E_\vartriangleright}{P^{(+365)}_\text{i}/P_\text{i}}-1$

Der χ- (Chi-) Effekt. Die AG Teil 1

Die Aufgabenstellung besteht also zunächst darin, objektiv vorliegende Zahlen (das ist ja der Trick bei der Sache 😉) in einen kausalen Zusammenhang zu stellen und zwar im zuvor definierten Sinne des $\chi_\text{u}$ -Koeffizienten:

Jahr	Wasser	Wind (on)	Wind (off)	Solar	Wasser	Windkraft	Solar	Windkraft	Solar
2009	5.34 GW	25.63 GW	0.06 GW	10.57 GW	19.00 TWh	38.61 TWh	06.60 TWh
2010	5.41 GW	27.01 GW	0.17 GW	17.94 GW	21.00 TWh	37.62 TWh	11.70 TWh	χ_u=+0.661	χ_u=+0.044
2011	5.63 GW	28.58 GW	0.19 GW	25.43 GW	17.67 TWh	49.86 TWh	19.60 TWh	χ_u=+0.570	χ_u=+0.182
2012	5.61 GW	30.56 GW	0.27 GW	33.03 GW	21.21 TWh	51.68 TWh	26.38 TWh	χ_u=+0.262	χ_u=+0.037
2013	5.59 GW	33.31 GW	0.62 GW	36.34 GW	22.85 TWh	52.74 TWh	31.01 TWh	χ_u=+0.067	χ_u=+0.000
2014	5.58 GW	37.56 GW	0.99 GW	37.90 GW	19.41 TWh	58.50 TWh	36.06 TWh	χ_u=-0.009	χ_u=+0.080
2015	5.59 GW	41.30 GW	3.28 GW	39.22 GW	14.44 TWh	80.62 TWh	36.46 TWh	χ_u=-0.042	χ_u=+0.071
2016	5.60 GW	45.28 GW	4.15 GW	40.68 GW	15.71 TWh	79.92 TWh	35.95 TWh	χ_u=-0.108	χ_u=-0.053
2017	5.60 GW	50.17 GW	5.41 GW	42.29 GW	15.57 TWh	105.69 TWh	37.15 TWh	χ_u=+0.164	χ_u=-0.046
2018	5.50 GW	52.45 GW	6.41 GW	45.31 GW	13.86 TWh	109.95 TWh	42.64 TWh	χ_u=-0.005	χ_u=+0.123
2019	5.50 GW	53.19 GW	7.53 GW	49.01 GW	16.33 TWh	125.89 TWh	43.57 TWh	χ_u=+0.056	χ_u=-0.050
2020	5.50 GW	54.84 GW	7.74 GW	54.07 GW	14.99 TWh	131.85 TWh	47.74 TWh	χ_u=+0.016	χ_u=-0.007
2021	5.50 GW	56.27 GW	7.77 GW	58.41 GW	19.69 TWh	113.51 TWh	48.45 TWh	χ_u=-0.159	χ_u=-0.060

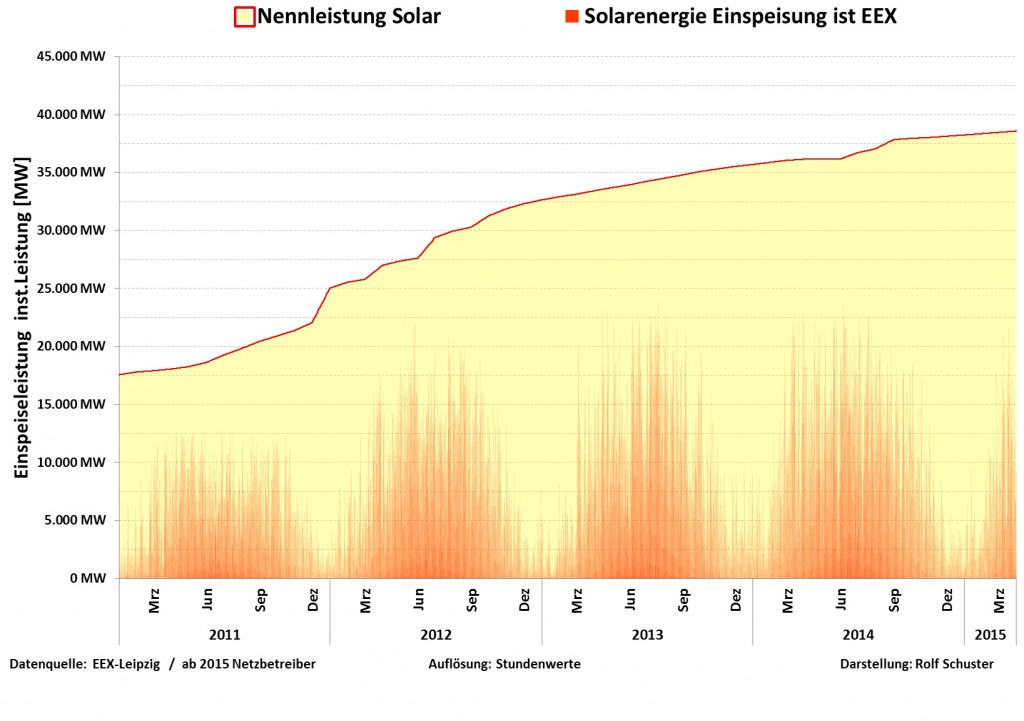
In der obigen Zusammenstellung ➡ betrachten wir zunächst die Spalten 2 bis 5, in denen die installierten Leistungen zum jeweiligen Jahresende ab anno 2010 für die einzelnen Energiearten festgehalten sind. Gleichen wir diese mit den Grafiken von „science-skeptical.de“ ➡ ab, so stellen wir fest, dass die in der Tat weitestgehend übereinstimmen.

➡ Quelle der Daten ist https://www.energy-charts.de/index_de.htm des Fraunhofer ISE
.

➡ Es wäre ohnehin eine Idee, diese Grafiken auf die Jahre 2015-2018 auszudehnen. Hierzu müssten wir jedoch erst die Einwilligung von science-skeptical.de bzw. der Urheber (Rolf Schuster?) einholen; mal sehen.
.

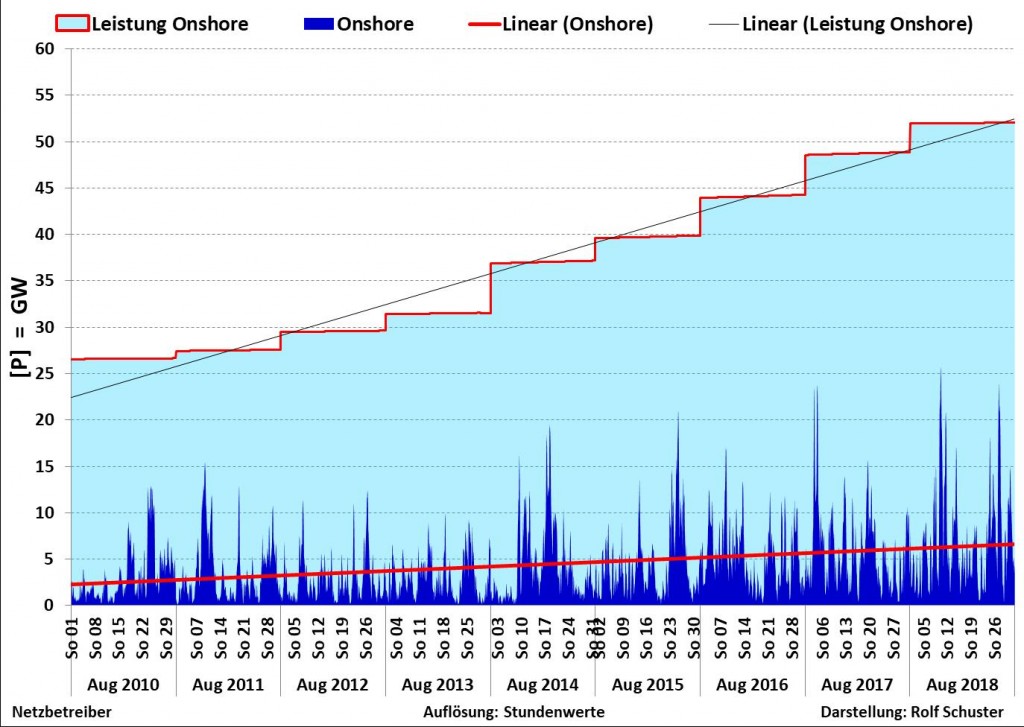
Leistung-Onshore-2010-2018 — Die Treppenlinie für die installierte Leistung der Onshore-Windkraft © Rolf Schuster.
Der zeitliche Zubau wird so viel exakter wiedergegeben.

Jedenfalls können wir die Angaben des ISE zur installierten Leistung als durchaus verlässlich ansehen und folgerichtig mit denen arbeiten. Denn erstens ist es relativ einfach, Nominalleistungen von Windrädern und Solaranlagen zusammen zu zählen und zweitens dürfte die Ökobranche wohl kaum darum bemüht sein, die installierte Leistung (und somit gewissermaßen die „eigene“ Leistung!) runter zu rechnen. Dies würde zwar den $\textstyle{\chi_\text{u}}$ künstlich aufbessern, aber so weit denken die Herrschaften ja nicht. Die EEG-Subventionen, die sich vorwiegend nach der installierten Leistung richten , scheinen da ausschlaggebender gewesen zu sein…

Viel problematischer ist es indes mit der effektiv „geernteten“ Energie $E_{\vartriangleright}$ . Denn hier bekommen wir zumeist die gesamte Palette an Mitteln der kreativen (Öko-) Statistik präsentiert. So wird unter der „Stromproduktion“ wirklich alles ausgewiesen, was eine Wind- oder Solaranlage verlässt – ja, mitunter auch noch jene „Energie“, die hätte eingespeist werden können, jedoch mangels Abnahmemöglichkeit nicht eingespeist werden konnte...😀. Es darf also nicht übersehen werden, dass hier jener Strom mit ausgewiesen wird, der zur Unzeit kommt und in jedem Falle einen zusätzlichen energetischen Aufwand erzwingt, z.B. in Form eines ineffizienten, da gedrosselten Betriebes von einem Kohlekraftwerk.

Wir schauen uns dennoch die Zahlen für Wind und Sonne ➡ mal an, auch wenn hier jegliche Pufferungseffekte außer Betracht bleiben und… staunen dabei nicht schlecht. Denn die Solarenergie beispielsweise weist zu Anfang der Dekade ein beständig positives $\textstyle{\chi_\text{u}}$ auf, was lediglich im Jahre 2011 nach oben und in 2013 nach unten – nachprüfbar witterungsbedingt – ausschlägt.

➡ Wasserkraft muss hier außer Betracht bleiben. Der Grund sind die infinitesimal kleinen Jahresschwankungen (mit Ausnahme des „Jahrhundertsommers“ 2018!), die im Sinne des Differenzenquotienten eine viel zu geringe Basis darstellen, als dass der Verlauf von 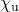$\textstyle{\chi_\text{u}}$ belastbar genug wäre. Mit Sicherheit würde hier das Gesetz der kleinen Zahlen durchschlagen.
.

Nun, zu erklären ist dieser durchweg positive Trend nur mit dem technischen Fortschritt und der damit verbundenen Effizienzsteigerung. Wow, möchte man meinen… aber leider drehte $\textstyle{\chi_\text{u}}$ in den gar nicht schlechten Solarjahren 2016/2017 ins Negative 😳 und selbst der Jahrhundertsommer 2018 brachte keine Jahrhunderternte ein ➡ – will heißen, dass der technische Fortschritt durch andere Negativeffekte aufgewogen und gar überholt wurde! Ob es damit zu tun hat, dass Schweizer Wissenschaftler gerade im Jahr 2017 einen EROI für PV von unter 1 ermittelt haben…?

➡ Wie extrem der Wetterausschlag in dem Jahrhundertsommer 2018 war, lässt sich am besten an dem völligen Einbruch der sonst relativ stabilen Wasserkraft ablesen. Vor diesem Hintergrund ist ein 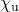$\textstyle{\chi_\text{u}}$ von +0.126 als jene berühmte Ausnahme zu werten, die die Regel bestätigt. Diesem Zusammenhang tragen wir durch eine entsprechende Kennzeichnung in der Tabelle Rechnung.
.

Bei der Windkraft hingegen wird’s noch krasser. Denn hier verschlechtert sich $\textstyle{\chi_\text{u}}$ kontinuierlich, von Jahr zu Jahr, dreht bereits 2014 ins Negative. Der Ausschlag im Ausnahme-Windjahr 2017 bricht den Trend nur scheinbar – schließlich folgte 2017 auf ein grottenschlechtes Vorjahr 2016 und das Folgejahr 2018 drehte erneut ins Minus (wenn auch knapp, dem Jahrhundertsommer sei Dank!). Der Negativtrend für die Windkraft ist somit ebenfalls bestätigt!

Ausblick auf AG Teil 2
.

Die AG wird weiterhin aktiv bleiben. Zum einen um den beobachteten Effekt in den Folgejahren zu verifizieren und zum anderen um die Pufferungseffekte zu erfassen. Letzteres dürfte wiederum viel Zeit in Anspruch nehmen, weil über Verluste nun einmal niemand besonders gerne spricht, der diese zu verantworten hat… Das eigentliche und abschließende Ziel dieser AG wird jedenfalls darin bestehen, den Verlauf des gepufferten Koeffizienten $\textstyle{\chi_\text{b}}$ zu untersuchen.

	Frage	Antwort
💡 1	Wie viele griechische Koeffizienten gibt es denn? Wie hängen $\textstyle{\chi_\text{.}}$ und $\textstyle{\kappa_\text{.}}$ zusammen? Was hat $\textstyle{\chi_\text{.}}$ mit dem EROI zu tun?	Nun, $\textstyle{\kappa_\text{.}}$ beschreibt das Verhältnis der beiden EROI’s – des ungepufferten zum gepufferten – hat also mit dem EROI und folglich mit der Gestehungs- und ggf. Pufferungsenergie zu tun. $\textstyle{\chi_\text{.}}$ hingegen hat mit installierter Leistung und folglich nur indirekt mit dem EROI zu tun: Die installierte Leistung korreliert zwar mit der Gestehungsenergie, aber eben nur schwach.
💡 2	Wenn der EROI die korrespondierende Bezugsgröße fürs $\textstyle{\kappa_\text{.}}$ ist, welche Größe ist es dan fürs $\textstyle{\chi_\text{.}}$ ?	Eine gute Frage . Man könnte von einem „Energy Return of Installed Power“ EROIP sprechen. Nicht zu vergessen ist aber, dass $\textstyle{\chi_\text{.}}$ die Fluxionen beschreibt, also die zeitlichen Veränderungen.

»

Motivation. Hintergründe

➡ Mit κ- (Kappa) wurde bereits im Teil 1 der AG „Erntefaktoren der Nord- und Ostsee Offshoreparks“ der dort postulierte „Pufferungskoeffizient“ bezeichnet und als das Verhältnis vom ungepufferten zum gepufferten EROI verstanden. .

Grundlegende Konzepte. Aufgabenstellung

➡ Unter „Fluxionen“ verstehen wir – nach guter alter Newton-Manier 😉 – schlicht Differential- bzw. Differenzenquotienten, also bzw. . .

➡ Wer mag, darf darin eine Parallele zur Heisenbergschen Unschärferelation sehen. Je genauer wir etwas verorten, auch zeitlich, umso unschärfer wird dessen Impuls und umgekehrt. .