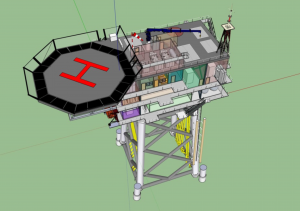
Offshore-Windkraft gilt als die Hauptsäule der „Energiewende“. Kolossal anmutende Offshore-Windparks wie etwa „Amrumbank West“ oder „Alpha Ventus“ sind dann auch begehrte Motive bei der Selbstdarstellung der Polit- und Wirtschaftsprominenz 😛 und ein Dauerschleife-Gegenstand einer euphorischen Berichterstattung in den (öko-lastigen  ) Medien. Doch leisten diese „Wunder der Technik“ wirklich jenen Beitrag zur energetischen Versorgung einer Volkswirtschaft, den deren schiere Monumentalität vielleicht vermuten lässt? Eine genauere Abschätzung der Erntefaktoren in der vorliegenden AG hat den in Teil 1 geäußerten Verdacht nun bestätigt: Der (gepufferte) EROI der Offshore-Windparks liegt deutlich unter 4. ) Medien. Doch leisten diese „Wunder der Technik“ wirklich jenen Beitrag zur energetischen Versorgung einer Volkswirtschaft, den deren schiere Monumentalität vielleicht vermuten lässt? Eine genauere Abschätzung der Erntefaktoren in der vorliegenden AG hat den in Teil 1 geäußerten Verdacht nun bestätigt: Der (gepufferte) EROI der Offshore-Windparks liegt deutlich unter 4. |
TE LE GR AM |
.

Pünktlich zu Neujahr 2016 ging der Teil 1 der AG-Energetik-Studie „Erntefaktoren der Nord- und Ostsee Offshoreparks“ zu Ende und zwar mit dem dort rudimentär errechneten Erntefaktor für den Offshore-Windpark „Amrumbank West“:
![]()
Die genauere Berechnung des EROI für die exemplarischen Offshore-Windparks „Amrumbank West“ bzw. „alpha ventus“ wurde indes auf den vorliegenden Teil 2 der Studie vertagt. Diese Berechnung gilt es nun nachzuholen.
Was den Teil 1 der Studie anbelangt, so haben wir immerhin über die rudimentäre Berechnung hinaus einige Interessante Entdeckungen gemacht. Zum einen haben wir gesehen, dass der EROI der Windkraft, bzw. der EE’s im Allgemeinen, mit sich weiterer verschlechterndem Energiemix (zulasten der Kernenergie !) immer weiter absacken wird. Ferner haben wir den Pufferungskoeffizienten κ eingeführt und für diesen festgestellt, dass er ebenfalls stark mit dem Energiemix „mitgeht“ und sich mit weiterem Ausbau der EE’s nur noch verschlechtern kann. Zu guter Letzt haben wir noch zahlreiche „Studien“ kennen gelernt, in denen der EROI von EE’s sogar im dreistelligen Bereich liegt – was angesichts selbst der noch so rudimentären Berechnung aus Teil 1 die Hände vors Gesicht schlagen lässt. Und wir haben einige derjenigen Tricks studiert, die dabei bemüht werden. Dazu zählen etwa das teilweise bis völlige Weglassen der Pufferung 😳 bzw. eine gezielte Fehlinterpretation des Carnot-Effektes – um nur diese zu nennen.
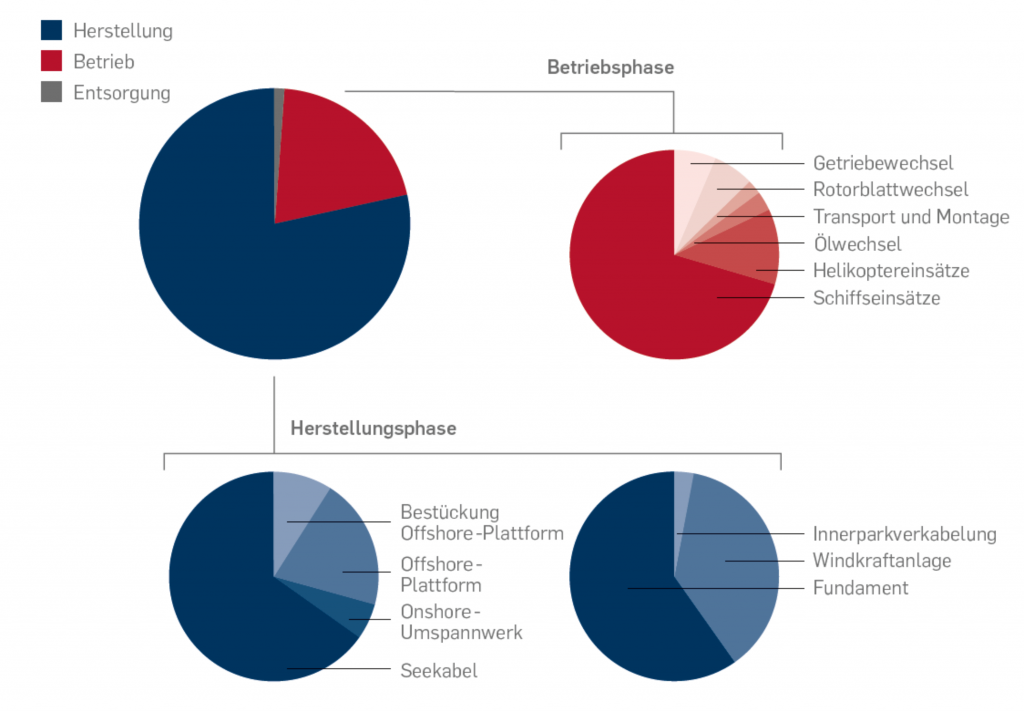
Die wesentliche Schwierigkeit, gegen die wir im Teil 1 der Studie immer wieder angerannt sind, bestand schlicht darin, an technische Daten etwa von „Amrumbank West“ (nachfolgend „AW“) bzw. „alpha ventus“ (nachfolgend „αv“) o.ä. heran zu kommen. Dies wiederum dürfte dem Umstand geschuldet sein, dass Studien wie diese von den Betreibern nicht gerade sehnsüchtigst erwartet werden, wie z.B. die Geschehnisse rund um die „E.ON SE-Zensur“ veranschaulichen mögen 😳, obwohl man hier sicherlich auch die Belange der Geheimhaltung wird gelten lassen können. Außerdem läuft „AW“ ja noch gar nicht richtig – insofern kann man das Fehlen der benötigten Angaben zum Teil auch so erklären. Jedenfalls enthält z.B. das Factsheet zu „AW“ überhaupt keine brauchbaren Infos.
Wie kann man aber Informationen bekommen, die gar nicht da sind, weil sie z.B. gar nicht da sein sollen? Nun, eines der Mittel hierzu und somit einer der wesentlichen Bestandteile der Methodik in der vorliegenden Studie besteht in der Extrapolation. Auf den knappsten Nenner gebracht handelt es sich um ein Hochrechnen von Daten von einem Windpark „X“ auf einen anderen Windpark „Y“ – vorausgesetzt, diese unterscheiden sich im Wesentlichen nur durch die Größe. In unserem Falle sind „AV“ und „αv“ zwei solche Windparks, wobei „αv“ bereits seit ein paar Jahren läuft und in der Zwischenzeit gar eine Studie zur ökologischen Auswirkungen an der Ruhr Universität Bochum erfahren hat. Die hier gewonnenen Erkenntnisse nahmen wir dankend an und verwenden diese in der vorliegenden Studie im Sinne der o.g. Extrapolation.
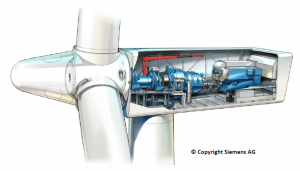
Et voila. Wir rechnen stets konservativ – frei nach dem Motto „in dubio pro Amrumbank West“. Jede Abrundung zugunsten von „AW“ kennzeichnen wir sodann mit „ “ um dem Leser nachher zu ermöglichen, Anhaltspunkte für einen möglicherweise noch niedrigeren EROI als errechnet einfach wiederfinden und zusammenzählen zu können.
“ um dem Leser nachher zu ermöglichen, Anhaltspunkte für einen möglicherweise noch niedrigeren EROI als errechnet einfach wiederfinden und zusammenzählen zu können.
Wir beginnen damit die gesamte investierte Energie ![]() für „AW“ (ungepuffert!) zu rechnen. Diese setzt sich zusammen aus dreierlei Komponenten:
für „AW“ (ungepuffert!) zu rechnen. Diese setzt sich zusammen aus dreierlei Komponenten:
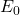 „Gestehungskosten“ ➡ des Windparks, bis hin zur Inbetriebnahme;
„Gestehungskosten“ ➡ des Windparks, bis hin zur Inbetriebnahme;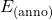 jährliche Betriebskosten, Wartung, externer Energiebezug;
jährliche Betriebskosten, Wartung, externer Energiebezug; Aufwendungen beim Abriss, Zuführung zum Recycling;
Aufwendungen beim Abriss, Zuführung zum Recycling;
➡ wenn von „Kosten“ die Rede ist, meinen wir stets die energetischen Aufwendungen
.
Somit gilt bei einer auf 20 Jahre angelegten Laufzeit:
![]()
Mit dem ersten Term tun wir uns ein wenig schwer. Zunächst werden die Gestehungskosten im Wesentlichen von den verarbeiteten Stoffen dominiert, wobei die jeweiligen KEA’s (kumulativer Energie-Aufwand) als relativ gut erforscht und folglich ziemlich genau bekannt gelten. Ein KEA gibt die gesamten energetischen Aufwendungen an, die aufzubringen sind, um einen bestimmten Werkstoff in den verarbeitungsfertigen Zustand zu bringen; beim Stahl etwa ist es dessen flüssige Form, die am Hochofen entsteht. Für die dominanten Stoffe sind folgende KEA’s bekannt:
- Stahl: 20 GJ/t (das sind die uns inzwischen bekannten : 5600 kWh/t):
- Kupfer: 40 GJ/t;
- Aluminium: 80.6 GJ/t;
Manche Stoffe sind deutlich im 3-stelligen Bereich, etwa die Refraktärmetalle.

Zu den wenigen gut bekannten Eckdaten betreffend „AW“ gehört eben die Menge vom verbauten Stahl, mit der sich E.ON zu brüsten pflegt: demnach sind’s „sagenhafte“ 100’000 t ! Aber Stahl ist eben nicht gleich Stahl… Bei „AW“ sind Kupfer, Aluminium sowie diverse Refraktärmetalle (etwa Molybdän) beigemischt. Die Beimischung beträgt zwar nur ein paar Prozent, aber die KEA’s von diesen Stoffen sind ja ungleich höher, als beim „normalen“ Stahl. Wenn wir hier auf die vollen 600 GWh aufrunden, dann entspricht es einer nur 3%-igen  Beimischung von einem Stoff mit einem KEA zwischen Kupfer und Aluminium. .
Beimischung von einem Stoff mit einem KEA zwischen Kupfer und Aluminium. .
Die restlichen Stoffe hingegen machen, lt. Hochrechnung von „αv“ und anderen Offshore-Parks, lediglich 18’000 t aus. Allerdings werden sie im wesentlichen von den hochenergetischen Stoffen dominiert, so dass wir einen KEA zwischen Kupfer und Alu ansetzen müssen. Folglich gilt:
![]()
Und sicherlich verbleiben wir immer noch im Bereich des Konservativen, wenn wir mit nur 9% Aufschlag  die Terrawattstunde voll machen und zwar für die Endproduktion der einzelnen Teile (normalerweise 10-15%):
die Terrawattstunde voll machen und zwar für die Endproduktion der einzelnen Teile (normalerweise 10-15%):
![]()

Soweit so gut – das gesuchte ![]() ist es noch lange nicht. Nun mögen die Transportkosten noch überschaubar sein und auch das Anbringen der Windturbinen mag sich im Rahmen halten bzw. in den obigen Aufschlag einfließen
ist es noch lange nicht. Nun mögen die Transportkosten noch überschaubar sein und auch das Anbringen der Windturbinen mag sich im Rahmen halten bzw. in den obigen Aufschlag einfließen  – das Hineinrammen der Monopiles in den Meeresboden ist es ganz bestimmt nicht mehr. Denn immerhin handelt es sich um monströse Rohre mit einem Durchmesser von 5 und Höhe von 60 Metern, die zur Hälfte in den Meeresboden hineingerammt werden müssen. Dies besorgt ein Hammer, der ein echter „Hammer“ 😉 ist: mit einer Wucht von 3000 t schlägt er alle 2 Sekunden auf den Monopile drauf und das bis zu 3000 mal! Da eine wie auch immer geartete Extrapolation von „αv“ wegen grundlegend unterschiedlicher Fundamente hinken würde, gilt es jetzt diesen Aufwand direkt zu errechnen:
– das Hineinrammen der Monopiles in den Meeresboden ist es ganz bestimmt nicht mehr. Denn immerhin handelt es sich um monströse Rohre mit einem Durchmesser von 5 und Höhe von 60 Metern, die zur Hälfte in den Meeresboden hineingerammt werden müssen. Dies besorgt ein Hammer, der ein echter „Hammer“ 😉 ist: mit einer Wucht von 3000 t schlägt er alle 2 Sekunden auf den Monopile drauf und das bis zu 3000 mal! Da eine wie auch immer geartete Extrapolation von „αv“ wegen grundlegend unterschiedlicher Fundamente hinken würde, gilt es jetzt diesen Aufwand direkt zu errechnen:
Die korrespondierende Fallhöhe bei 30 Schlägen pro Minute beträgt:
![]()
Somit wird bei jedem Schlag der Wucht von 3000 t die folgende Potentialenergie an den Monopile übergeben:
![]()
Jetzt müssen nur noch diese Energie mal 3000 Schläge und dann mal 80 Monopiles nehmen:
![]() ➡
➡
➡ Aufwendungen im Zusammenhang mit Umweltauflagen, insb. zur Minderung des horrormäßigen Hydroschalls von 240 dbA lassen wir hier außer Betracht.  E.ON spricht von 30 Mio € Zusatzaufwand in diesem Zusammenhang – s. auch „Untersuchung und Erprobung von Hydro‐Schall‐Dämpfern (HSD) zur Minderung von Unterwasserschall bei Rammarbeiten für Gründungen von OWEA“
E.ON spricht von 30 Mio € Zusatzaufwand in diesem Zusammenhang – s. auch „Untersuchung und Erprobung von Hydro‐Schall‐Dämpfern (HSD) zur Minderung von Unterwasserschall bei Rammarbeiten für Gründungen von OWEA“
.
Folgerichtig erhalten wir das gesuchte ![]() .
.
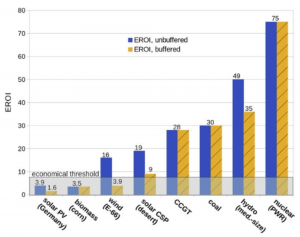
Bei dem zweiten Term machen wir es uns etwas einfacher. Denn die Extrapolation von „αv“ ergibt relativ klare ![]() , wobei wir hier weder den externen Energiebezug ➡ berücksichtigen
, wobei wir hier weder den externen Energiebezug ➡ berücksichtigen  noch den Ermüdungseffekt der Anlagen ➡ mitrechnen
noch den Ermüdungseffekt der Anlagen ➡ mitrechnen  .
.
➡ Windkraft-Anlagen sind auf Energiezufuhr von außen angewiesen – etwa für die Steuerung, Controlling, Kühlung, Anti-Korrosionsmaßnahmen – um nur diese zu nennen. All diese Maßnahmen müssen auch bei Windflaute aufrecht erhalten werden, weshalb eine „Selbstversorgung“ nicht in Frage kommt.
.
➡ Windkraft-Anlagen lassen nach 10, spätestens 12 Jahren spürbar nach. so dass sich die wartungsbedingten Standzeiten dramatisch erhöhen und somit auch automatisch die wartungsbedingten Aufwendungen.
.
Zu guter Letzt bleibt noch der Abriss. Hier gehen wir ebenfalls nicht über die „αv“-Extrapolation hinaus  , allerdings rechnen wir noch einmal die RAM-Energie dazu, da die Beseitigung der Monopiles sicherlich nicht weniger Energie kosten wird:
, allerdings rechnen wir noch einmal die RAM-Energie dazu, da die Beseitigung der Monopiles sicherlich nicht weniger Energie kosten wird:
![]()
Summa summarum erhalten wir:
![]()
Was bleibt ist nur noch das ![]() . E.ON will zwar sagenhafte
. E.ON will zwar sagenhafte ![]() pro Jahr „ernten“, doch dies ist vollkommen unrealistisch. Denn zum einen kennen wir unseren Betzschen-Effekt und zum anderen die Ermüdung die ab dem 10. Betriebsjahr einsetzt. Wenn wir hier nur 10% abziehen, dann ist es einen
pro Jahr „ernten“, doch dies ist vollkommen unrealistisch. Denn zum einen kennen wir unseren Betzschen-Effekt und zum anderen die Ermüdung die ab dem 10. Betriebsjahr einsetzt. Wenn wir hier nur 10% abziehen, dann ist es einen  allemal wert und „AW“ ist damit noch gut bedient. Wir puffern es dann noch mit dem Faktor 4.1 ab und erhalten:
allemal wert und „AW“ ist damit noch gut bedient. Wir puffern es dann noch mit dem Faktor 4.1 ab und erhalten:
![]()
woraus der EROI ![]() resultiert. ¶
resultiert. ¶
Schlussfolgerungen:
- Zunächst können wir mit Fug und Recht festhalten, dass unsere vorliegende Studie die Vorstudie nicht falsifiziert hat. Denn das Resultat
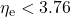 widerlegt ja
widerlegt ja 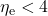 nicht sondern verschärft die Aussage sogar. Indes liefert die Studie keine brauchbare Stütze für die weitaus schärfere Vermutung von
nicht sondern verschärft die Aussage sogar. Indes liefert die Studie keine brauchbare Stütze für die weitaus schärfere Vermutung von 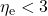 . Denn dazu müssten alle Green-Smileys
. Denn dazu müssten alle Green-Smileys  „dicke“ zutreffen und gar keine Pendants wiederum zulasten von „AW“ haben, was jedoch den Lebenserfahrungen mit derartigen Studien widerspricht. Wir gehen vielmehr davon aus, dass wir uns hier und da mal verrechnet haben werden und um dies zu kompensieren haben wir eben etliche
„dicke“ zutreffen und gar keine Pendants wiederum zulasten von „AW“ haben, was jedoch den Lebenserfahrungen mit derartigen Studien widerspricht. Wir gehen vielmehr davon aus, dass wir uns hier und da mal verrechnet haben werden und um dies zu kompensieren haben wir eben etliche  gesetzt;
gesetzt;
- Unsere Näherungswerte waren zwar nicht immer exakt, jedoch haben sich die Abweichungen per Saldo größtenteils aufgehoben. So haben wir z.B. in der allerersten Version der Vorstudie einen zu hohen Wert für restliche Stoffe angesetzt – auf der anderen Seite die Beimischung hochenergetischer Metalle im Stahl außer Betracht gelassen. Dennoch ergab sich hieraus eine Korrektur unserer Näherungswerte um ca. 10% zugunsten von „AW“;
- Allerdings, was unsere Studie eindeutig falsifiziert hat, sind eine ganze Reihe von Studien, Publikationen etc. die einen EROI im 2- oder gar 3-stelligen Bereich 😳 belegt haben wollen. Es ist für uns absolut nicht nachvollziehbar, wie ein mit Hochschultiteln vollgespicktes Forscherteam angesichts solch fundamentaler mathematischer und technischer Zwänge allen Ernstes eine energetische Amortisationszeit von nur wenigen Wochen 😳 vertreten kann.
