Nach der Erstveröffentlichung des „Algorithmus zur quantenmechanischen Datenübertragung“ – seinerzeit noch unter der Bezeichnung „EPR“ – am 2. März 2017, erfuhr ich aus dem Netz ein Feedback, was ich eingedenk der „Trockenheit“ der Materie so nicht erwartet hätte. Überrascht hat mich vor allem das häufig geäußerte „faszinierend!“ – auch und gerade von denjenigen, die ansonsten in einer unnachahmlichen Freimütigkeit zugaben, nicht allzu viel davon verstanden zu haben.

Ich persönlich kann mir diese doch recht überraschende Reaktion nur dadurch erklären, dass die Aussicht auf eine Datenübertragung mit Überlichtgeschwindigkeit bzw. über einen abhörsicheren „Kanal“ eben jene Faszination hervorruft, die die Hemmschwellen zur Quantenmechanik bzw. gar Quanteninformatik etwas absinken lässt. So wird im Allgemeinen gespannt zugehört, man lässt sich alles noch mal und noch mal erklären, man schreckt nicht vor jeder banalen mathematischen Gleichung in einem Beitrag zurück (ein Effekt, den ansonsten jeder Buchverlag zu Genüge kennt 😉) usw. Und so möge der vorliegende Beitrag auf der einen Seite ein Leitfaden für den Verfasser sein, der seine Gedanken bei diversen Events vortragen darf – auf der anderen Seite aber ein Stoff zum Nachlesen für all diejenigen, die diesen Events nicht haben beiwohnen können und evtl. vorhaben, welche anzuberaumen.

Zusammenfassung (Abstract) 

.
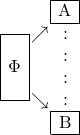  Dabei sind die Photonenpaare quantenmechanisch verschränkt:  

Das QKD-Verfahren (Quantum Key Distribution) ➡ sieht vor, verschränkte Photonenpaare nach A und B („Alice“ und „Bob“) zu übertragen und die mittels Bellscher Messung gewonnenen Basiszustände als Bits eines symmetrischen kryptographischen Schlüssels zu nutzen. Die Polarisationsebenen werden dabei auf beiden Seiten rein zufällig zwischen zwei oder mehr Varianten gewählt (etwa 0°/120°/240°) und die getroffene Wahl wird auf klassischem Wege zwischen A und B gegenseitig ausgetauscht. Auf die Art und Weise wird es möglich, die Bellsche Ungleichung zu verifizieren, so dass im Anschluss an ein solches Prozedere entschieden werden kann, ob der Schlüssel zuvor womöglich „angeschaut“ worden sein könnte und ob man ihn folglich verwenden darf oder nicht.

Das hier vorgestellte QDD-Verfahren (Quantum Data Distribution) sieht hingegen vor, die mittels Bellscher Messung gewonnenen Basiszustände direkt als Datenbits zu nutzen und zwar ohne Verschlüsselung 👿. Die Auswertung der Bellschen Ungleichung erfolgt bereits während der Datenübertragung und führt ggf. zur deren Terminierung.

➡ Das QKD-Verfahren geht auf eine Idee des Physikers Artur Ekert aus dem Jahre 1991 zurück.
.

Grundlegende Konzepte
.

Um das was nun folgt besser nachvollziehen zu können, sind zumindest rudimentäre Kenntnisse von grundlegenden quantenmechanischen Konzepten überaus hilfreich. Von daher sei nicht nur den Einsteigern das nebenan verlinkte Youtube wärmstens empfohlen. Anhand eines Klassikers der Quantenmechanik, nämlich des Doppelspaltexperimentes, werden Konzepte, wie Quantenzustand, Basisvektor, Superposition, Verschränkung, (Bellsche) Messung, Nichtlokalität bis hin zur „spukhaften Fernwirkung“, also dem EPR-Phänomen etc. erklärt und mit ausgefeilten Computer-Animationen sehr anschaulich dargelegt.

Fürs Studium der beiden hier diskutierten „Q“-Verfahren – des QKD sowie des QDD – benötigen wir insbesondere die Superposition sowie Verschränkung von Photonen bzw. Photonenpaaren und zwar anhand der Observablen (Beobachtungsgröße) „Polarisation“. Ferner benötigen wir den zuvor erwähnten EPR-Effekt (Einstein-Podolsky-Rosen), den der erstere seinerzeit als „spukhafte Fernwirkung“ 😈 (spooky action at a distance) bezeichnete. Gerade diese „spukhafte Fernwirkung“ ist es, die im Rahmen der beiden „Q“-Verfahren zwecks Datenübertragung genutzt wird. Wir sprechen vom „EPR-Kanal“… Aber langsam – eins nach dem anderen.

Nun haben wir aus dem obigen Doppelspaltexperiment gelernt, dass man einem Photon bestimmte (Basis-) Zustände hinsichtlich einer Observablen zuordnen kann und dass diese – wie im vorliegenden Beispiel – schlicht die Nummer desjenigen Spaltes sein kann, den das Photon passiert: Spalt 1 oder Spalt 2, also z.B. 0 oder 1. Wir wissen ferner, dass solange das Photon nicht beobachtet, also nicht „gemessen“ wird, es sich irgendwie ➡ in einer bizarren Überlagerung (Superposition) der Basiszustände befinden kann und dass es sofort genau einen dieser Zustände einnimmt, sobald es auch nur passiv beobachtet wird.

➡ Um dieses „irgendwie“, also um den bizarren Quantenzustand, ranken sich Legenden bis hin zu regelrechten Philosophien. So erklärt beispielsweise die sog. Kopenhagener Interpretation (deren Ziehvater war Niels Bohr) die Frage nach dem Wesen eines Teilchens, das sich in Superposition befindet, für sinnlos… 😮
.

Die tensorbasierte Notation für diesen Sachverhalt, die sog. „Ket“-Notation, lautet:

Wir lassen hier außer Betracht, dass es sich bei a und b um komplexe Zahlen handelt und wir uns in einem sog. Hilpert-Raum bewegen. Für unsere Betrachtungen genügt es vorauszusetzen, dass die Quadrate dieser Koeffizienten die Wahrscheinlichkeiten für die Einnahme der jeweiligen Basiszustände infolge einer Messung bedeuten. Deshalb müssen diese zur 1 aufsummieren. So gesehen könnte man ein „Dreispalt-Experiment“ folgendermaßen beschreiben:

Für ein Photonenpaar gilt dann logischerweise:

Soweit so gut. Jedoch im Jahre 1935 postulierten eben Albert Einstein, Boris Podolsky und Nathan Rosen, dass es Teilchenpaare geben kann, für die gilt, also die beiden letzten Terme verschwinden:

Bei näherem Hinsehen ist es schier unglaublich! Denn es würde ja bedeuten, dass beide Teilchen perfekt korreliert wären (Erwin Schrödinger: „Verschränkung“) – soll heißen, dass eine Messung an einem der beiden Photonen stets das gleiche Resultat bei dem anderen hervorbringen würde… 👿 ?! Und das mit sofortiger Wirkung, unabhängig davon, wo sich beide Teilchen gerade befinden mögen?

Albert Einstein, der sich zeit seines Lebens nicht mit den Implikationen des eigens entdeckten Phänomens anfreunden konnte, sprach unbeirrt von „spooky action at a distance“ und ebenso die Fachwelt redete, zumindest anfänglich, vom „EPR-Paradoxon“. Doch mittlerweile, nach mehrfacher experimenteller Bestätigung diees Phänomens, spricht man doch eher vom „EPR-Effekt“ und in der Quanteninformatik eben vom „EPR-Kanal“. Diesen virtuellen „Kanal“ machen sich die beiden hier diskutierten „Q“-Verfahren zunutze.

Das EPR-Phänomen
.

Nachdem wir den mathematischen Gedankengang von Einstein, Podolsky und Rosen rudimentär nachvollzogen haben, sind wir doch stark geneigt zu sagen, wie bitte?? Eine Zustandsveränderung an einem Teilchen soll sich auf ein u.U. Lichtjahre entferntes Teichen auswirken und zwar sofort, mit quasi unendlicher Geschwindigkeit?

Es würde den Rahmen dieses Vortrags sprengen, all die möglichen (Ver-) und Erklärungen für das EPR-Phänomen zu erörtern – von einem „mathematischen Paradoxon“ bis hin zu den versteckten Variablen. Tatsache bleibt, dass man heute nicht mehr von einem „Phänomen“ spricht, sondern mehr von einem (EPR-) Effekt, und zwar von einem mehrfach experimentell bestätigten Effekt. Denn in der Tat sind inzwischen technische Verfahren entwickelt worden, die verschränkte Photonen erzeugen und diese dann an beliebig weit voneinander entfernte Orte A und B transferieren können. Und weil die Zustandsveränderung von A nach B „sofort“ repliziert wird, kann man mit Fug und Recht von einer Informationsübertragung von A nach B mit unendlicher Geschwindigkeit sprechen… über einen virtuellen EPR-Kanal!

Allerdings muss ich die Euphorie in Sachen Überlichtgeschwindigkeit an dieser Stelle gehörig bremsen. Denn zunächst einmal ist eine Verbringung von verschränkten Photonen zu Alice und Bob vonnöten, was höchstens mit Lichtgeschwindigkeit geht ➡ und zum anderen ist der Ausgang jedweder Messung vollkommen ungewiss: 0 oder 1 – zwar bei A und B gleich, aber eben 0 oder 1 und nichts Genaueres. So ähnlich verhält es sich mit den Augenpaaren: solange sie einem und demselben Menschen gehören, wissen wir, dass sie die gleiche Farbe haben. Aber welche es konkret ist, das wissen wir solange nicht, bis wir diesem Menschen eben in die Augen schauen. Erwin Schrödinger sagte seinerzeit dazu: „Maximales Wissen über ein zusammengesetztes System bedeutet nicht notwendigerweise ein maximales Wissen über dessen Einzelteile“. 💡

➡ Es handelt sich dabei nicht nur um eine Verbringung von Teilchen als Informationsträgern zu A und B, sondern auch und insbesondere um die Information selbst. Denn diese Information ist nicht klassisch in Bits und Bytes fassbar, wenngleich sie in den Korrelationen drinnen steckt! Aus diesem Grunde ist es nicht möglich, zwei bereits räumlich voneinander getrennte Teilchen miteinander zu verschränken, denn dies würde einen Verlust der Information bedeuten, den es aber nicht geben kann, wie wir spätestens aus dem Vortrag über das Informationsparadoxon wissen.
.

So gesehen dürften die Vorteile der beiden „Q“-Verfahren – QKD und QDD – wohl eher in deren Sicherheit zu suchen sein, als in der so sagenhaft klingenden „Überlichtgeschwindigkeit“. Außerdem legen die Erfahrungen mit Datenübertragungs-Protokollen den Schluss nahe, dass wir auch bei den beiden vorliegenden „Q“-Verfahren um einen umfangreichenden begleitenden Datenaustausch auf konventionellem Wege kaum umhinkommen werden. Dies ist bereits bei dem von Ekert vorgeschlagenen QKD-Verfahren der Fall, wie wir nachfolgend sehen werden.

Bellsche Ungleichung
.

Wie wir zuvor gesehen haben, ist es doch irgendwie möglich, Informationen von A nach B zu übertragen und zwar sofort und ohne dass ein physikalisches Signal von A nach B gesendet wird – zwar mit der Beschränkung auf den korrelativen Teil der Information und deren Vorab-Verbringung an A und B – aber sonst funktioniert es in diesem Sinne schon. Unser ominöser EPR-Kanal hat in der Tat einen unendlichen Durchsatz und ist mit keinen Mitteln abzuhören. Doch was passiert, wenn der Spion nicht zwischen A und B sitzt und seine Füller ausstreckt, sondern zwischen Φ und A oder gar direkt „vor Ort“ ? Fürwahr eine grauenvolle Vorstellung, denn damit würde er ja jeder Messung zuvorkommen und wir würden „seine“ Messresultate für bare Münze nehmen… 😈

Die Frage ist nun, welche Möglichkeiten wir haben dies festzustellen (oder auszuschließen), wenn jedes noch so passive Anschauen eines Photons bereits dessen Messung bedeutet?

Betrachten wir noch einmal die Photonen mit deren Observablen „Polarisation“. Befindet sich ein Photon in Superposition, so ist die Wahrscheinlichkeit einen Polarisator zu passieren bzw. „ausgelöscht“ zu werden „fifty-fifty“ und zwar unabhängig von der Wahl der Polarisationsebene:

Sitzen wir jetzt mit unserem Polarisator hinter dem Spion, so kriegen wir mit der gleichen Wahrscheinlichkeit 0 oder 1 weitergereicht und bekommen folglich die „Vorab-Messung“ gar nicht mit. Drehen wir aber den Polarisator um den Winkel θ gegenüber demjenigen des Spions, so verringert sich die Wahrscheinlichkeit ein Photon „abzukriegen“ (also die 1 durchgereicht zu bekommen) gem. Gesetz von Malus:

Mit anderen Worten, wir können einem Photon bzw. Photonenpaar zwar nicht ansehen, ob es zuvor gemessen worden ist oder nicht, aber wir können es mit einem Photonenstream sehr wohl tun und zwar anhand von statistischer Auswertung der Messdaten von hinreichend zahlreichen Teilchen. Es handelt sich hierbei um die sog. Bellsche Ungleichung.

Quantum Key/Data Distribution QKD/QDD 
.

  Dabei sind die Photonenpaare quantenmechanisch verschränkt:  

Die Grundidee des QDD-Verfahrens besteht darin, die an den Photonenpaaren ermittelten Werte nicht als Bits eines kryptographischen Schlüssels zu verwenden (QKD-Verfahren), sondern als Bits des von A nach B zu übermittelnden Inhalts. Da diese Bits rein zufällig sind, ist jeweils ein Korrekturbit zu übermitteln. Die Prüfung der Bellschen Ungleichung muss – im Gegensatz zum QKD-Verfahren – stets kontinuierlich erfolgen. Im Falle eines positiven Befundes wäre die Übertragung sofort zu stoppen.

Das Protokoll für beide Algorithmen würde in etwa folgendermaßen aussehen:

foreach(øA,øB) { // für jedes Photonenpaar

set θA=random(Θ),θB=random(Θ) // A&B wählen eine zufällige Polarisationsebene aus, machen jeweils eine Messung und teilen sich gegenseitig die Polarisationsebenen mit

if (θA==θB) { // Polarisationsebenen gleich

// QKD: das gemessene Bit wird zum kryptographischen Schlüssel hinzugefügt
// QDD: das gemessene Bit wird zum Übermittlungssatz hinzugefügt und mit einem Korrekturbit versehen

}
else { // Polarisationsebenen ungleich

// A und B teilen sich die Messresultate mit zwecks Auswertung der Bellschen Ungleichung

}

} // endof foreach

Es ist absolut trivial zu zeigen, dass beide Verfahren einwandfrei funktionieren und dass deren Komplexität praktisch gleich ist… wenn – und das ist der Casus Knacksus – wenn man einmal von der Auswertung der Bellschen Ungleichung absieht. Dass mit dieser Auswertung buchstäblich alles steht und fällt, sieht man spätestens am Vorgang der Messung. Denn hat irgendjemand eines der Photonen auch nur angeschaut, hat er die Verschränkung des Photonenpaars zerstört und somit ist die Annahme, dass A und B das gleiche Resultat messen würden, nicht mehr zutreffend. Mit anderen Worten, der EPR- (Daten-) Kanal würde die Daten verfälschen, was einem Garaus für beide „Q“-Verfahren gleichkäme.

Jedoch während das QKD-Verfahren eine relativ einfache Möglichkeit bietet, die Bellsche Ungleichung zu prüfen – nämlich nach der Erzeugung des Schlüssels, bevor man entscheidet, ihn zu verwenden – ist es bei dem QDD-Verfahren ein Bit komplizierter. Denn diese Prüfung muss ja während der Datenübertragung kontinuierlich laufen. Die Frage, die sich dabei aufdrängt, ist, ob es dann nicht evtl. schon zu spät ist, wenn wir den Spion ausgemacht haben. So richtete ich seinerzeit in meiner Erstveröffentlichung des QDD-Algorithmus eine Bitte an die „Y-Generation“ mir bei diesem Beweis zu helfen, aber leider hielt sich der Zustrom an Vorschlägen sehr in Grenzen 😉. Nachfolgend will ich den Beweis dafür nachliefern, dass auch das QDD-Verfahren gegenüber dieser Art von Attacken hinreichend sicher ist.

➡ Es großes, allerdings gemeinsames Problem beider „Q“-Verfahren besteht darin, dass ein Spion einige Bits verfälschen kann ohne entdeckt zu werden. Er kann sozusagen unter dem Bellschen Radar durchschlüpfen. Hierauf sollte im kommenden Kapitel noch genauer eingegangen werden.
.

Im folgenden gehen wir von einer kontinuierlichen Messung an den Photonen aus. Denn eine partielle Messung, also nur einige Bits, bringt einem Spion nichts (was nutzen einem schon zwei Bits aus einem Byte?), außer dass er den Ablauf nachhaltig stören kann. Letzteres würde eine andere Art der Attacke bedeuten, gegenüber der allerdings beide „Q“-Verfahren gleichermaßen anfällig sind; dazu gleich mehr.

Zwecks Vereinfachung der Beweisführung setzten wir Voraus, dass es nur zwei Polarisationsebenen gibt, die orthogonal (also senkrecht) zueinander liegen. Misst jetzt der Spion eine 1, so wird die bei mir aber komplett ausgelöscht: . Der Erwartungswert der Messung halbiert sich so auf 0.25. Die Frage ist, ab wann dieser Wert feststellbar ist, so dass man Alarm schlägt und die Übertragung unterbricht. Mit anderen Worten, es ist die Frage nach dem Konfidenzintervall.

Eine einfache Überlegung zeigt, dass die Chancen bereits ein 16-Bit-Register mitzulesen ohne unseren Verdacht zu erregen infinitesimal klein sind. Denn der Spion müsste mehrere Male hintereinander die Polarisationsebene richtig erraten, was umgekehrt exponentiell gegen die Null geht. Er hätte also allenfalls die Chance, einige wenige Zeichen einer Message mitzulesen, bevor er entdeckt wird.

Grenzen der „Q“-Verfahren
.

Abschließen will ich den Vortrag mit einer Kuriosität um Anton Zeilinger, den österreichischen Dauerkandidaten auf den Physik-Nobelpreis. Zeilinger hat wie kein anderer – vielleicht neben Rainer Blatt – praktische Implementierungen von Quantencomputing, Quantenkryptographie etc. auf den Weg gebracht hat und beispielsweise zuletzt, am 29.09.2017, ein Telefonat mit Hilfe einer QKD-erzeugten Verschlüsselung durchgeführt.

Was ihm aber wohl eher den längst überfälligen Nobelpreis eines Tages einbringen dürfte, ist vielmehr die Entdeckung des sog. GHZ-Effektes (Greenberger, Horne, Zeilinger). Dieser Effekt, der sich wirklich auf die wunderschön kompakte Form runterbrechen lässt:

zeigt gleichzeitig eine dicke Sicherheitsschwäche von „Q“-Verfahren auf. Denn sollte sich ein Spion jeweils ein drittes Photon zu sich schicken lassen, ist alles buchstäblich im Eimer… 😆

 

.

.